Introduzione e Classificazione sistemi ⚙️

L'automazione si occupa di imporre a dei sistemi un certo andamento o comportamento desiderato.Con sistemi intendiamo parti della realtà che ci interessano, per esempio se prendiamo delle pale eoliche, uno dei problemi di controllo che si possono avere è tenere sotto controllo la velocità con cui ruotano le pale(nell'esempio dell'eolico), oppure in un aereo, il problema di imporre un certo andamento in termini di velocità verticale, direzione, potenza dei motori per esempio, oppure un'azienda, quando voglio controllare per esempio i costi di produzione ecc...

Invece il regolatore è quel componente che vogliamo progettare che agisce sul sistema per farlo comportare nel modo desiderato.Esso agisce sulle variabili di controllo (nel cruise control è la pressione sull'acceleratore ad esempio), e la modifica di queste variabili mostra in uscita un cambiamento sulle variabili che vogliamo controllare, le variabili controllate appunto (la velocità della macchina).

Come vedremo la velocità della macchina(misurata da qualche sensore), che è l'uscita(output) del nostro sistema deve essere "letta" dal nostro regolatore(cruise control) in modo che esso sappia se sta dando la pressione giusta al pedale dell'acceleratore o meno e quindi fare aggiustamenti.Il fatto che l'uscita venga riportata in ingresso si chiama RETROAZIONE e diremo che il nostro sistema è in anello chiuso,più in avanti vedremo meglio cosa vuol dire.

Individuato il sistema, è poi essenziale utilizzare un modello matematico che ne descriva il comportamento, selezionando le variabili che danno più informazioni di interesse(ad esempio, nel cruise control, non mi interessano variabili come la temperatura, ma mi interesserà la velocità, la pendenza della strada ecc...). Quindi bisogna scrivere le equazioni che descrivono il comportamento di questo sistema.



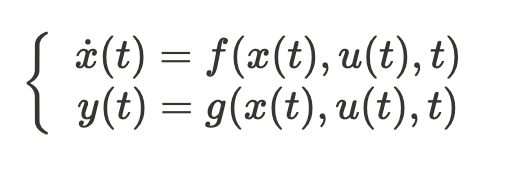
Iniziamo ora a vedere a livello matematico come si rappresenta un sistema.Come si può vedere, un sistema andrebbe scritto in questo modo. x è detto stato del sistema e rappresenta una descrizione completa delle condizioni del sistema in un dato momento.Cioè lo stato ci dice internamente in che situazione si trova il sistema. E' un concetto poco chiaro all'inizio, ma si pensi all'energia di un condensatore in un circuito elettrico: istante per istante possiamo considerarlo come quella variabile che caratterizza il sistema in quel momento.Dallo stato sono in grado di vedere anche il comporamento futuro del sistema.Di solito ci sono equazioni differenziali a definirlo, come si vede nel sistema di sopra.

f è la relazione(cioè la funzione matematica,l'espressione) che lega lo stato alla sua derivata, y è la trasformazione d'uscita, cioè la relazione tra gli ingressi u(t) e lo stato ed è quindi l'output del nostro sistema.La t tra parentesi indica che quella è una funzione del tempo, cioè che il suo valore varia nel tempo(ad esempio se voglio il suo valore dopo 2 secondi, dico u(2)).

In particolare, vogliamo che l'uscita del sistema(la velocità della macchina nel nostro esempio del cruise control), vada come il nostro segnale di riferimento chiamato w(t), che ad esempio potrebbe essere una funzione costante, o anche qualcosa fatto cosi:



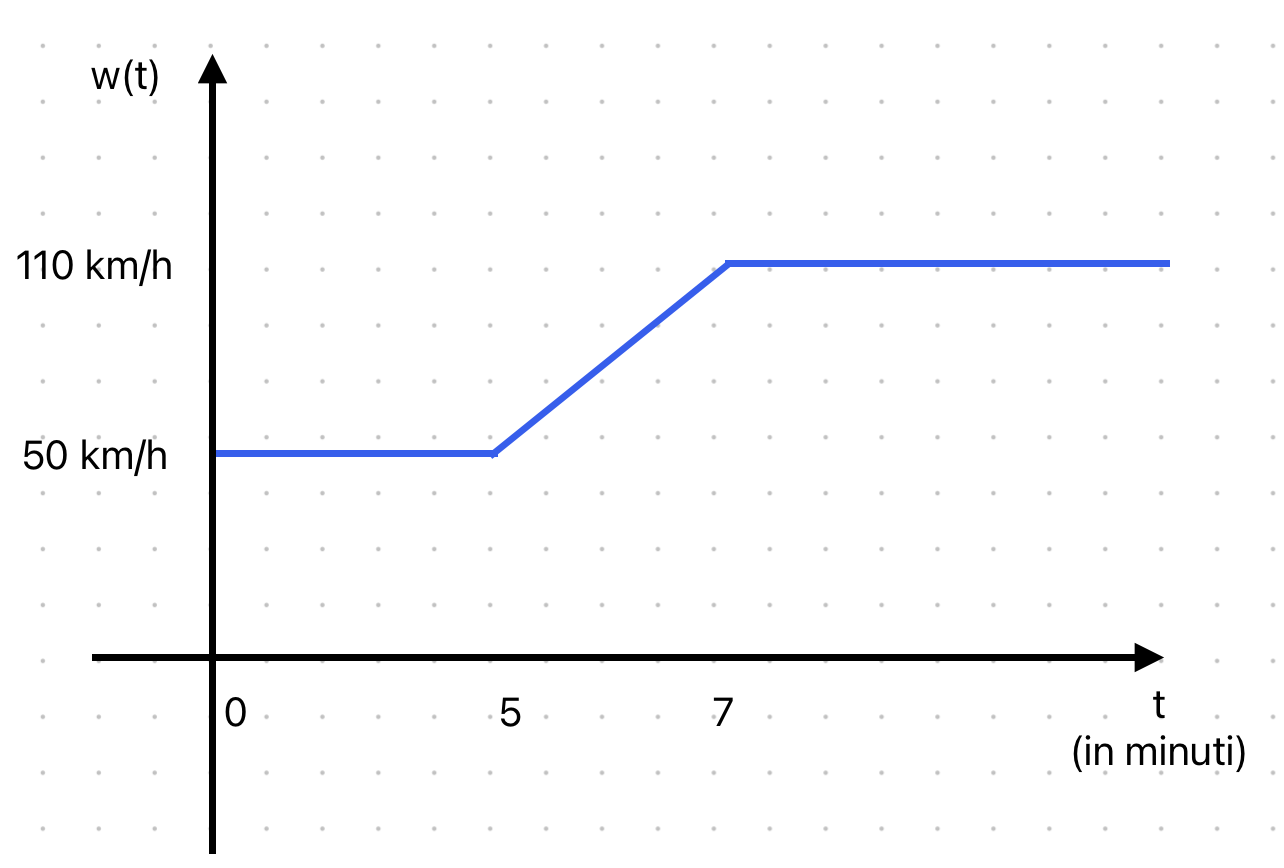
immaginiamo che all'inizio siamo su un tratto di strada che ha limite 50 km/h e poi però vogliamo andare più veloci, dopo 5 minuti.Allora all'istante 5 dobbiamo far si che il nostro controllore faccia accelerare la macchina fino a portarla a 110 ad esempio.Questo è ciò che vorremmo, cioè w(t), ma nella realtà pratica non è mai cosi, y(t) differisce sempre un po' dal segnale ideale di riferimento,perchè agiscono disturbi(ce ne sono diversi, ma uno nel nostro caso potrebbe essere l'inclinazione della strada, perchè ogni volta che cambia la pendenza dobbiamo riaggiustare la pressione sull'acceleratore). L'uscita reale potrebbe essere questa:



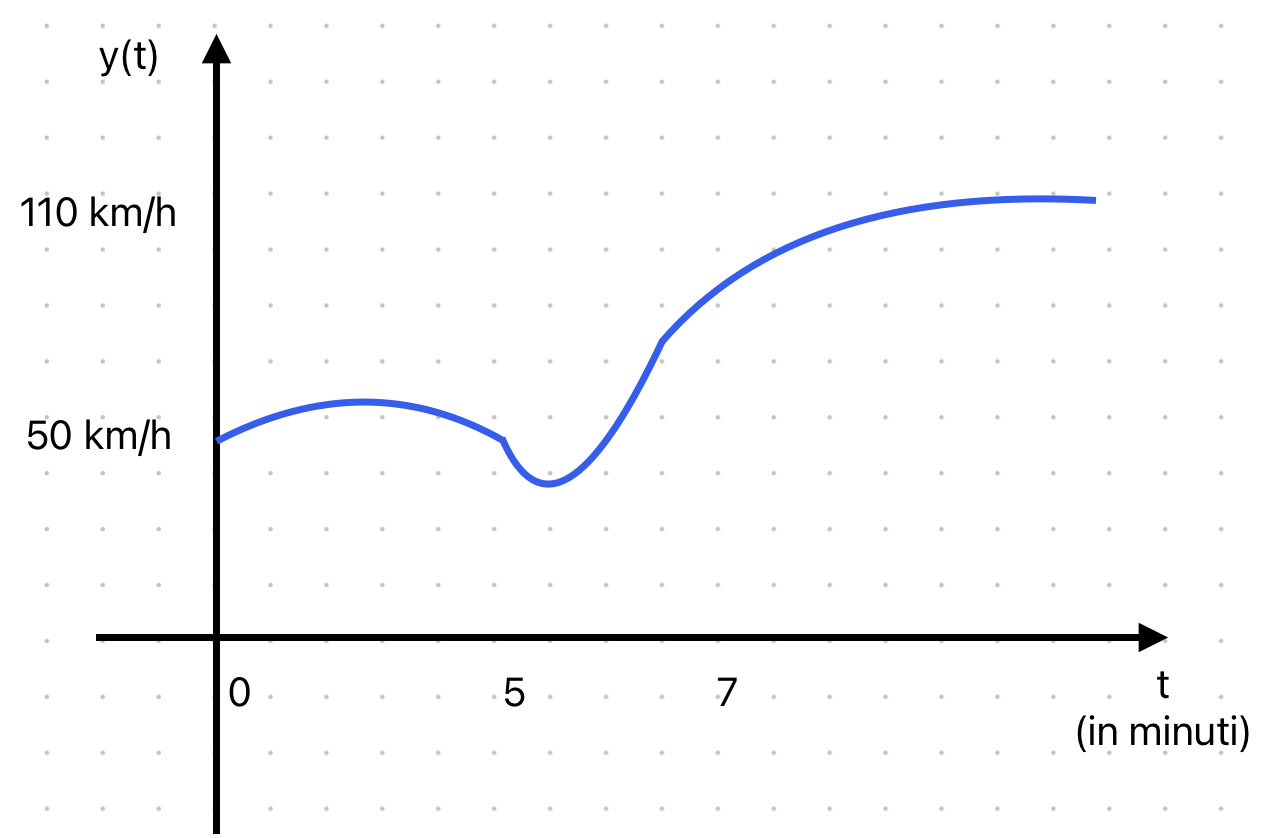
Definiamo a questo punto un concetto molto importante, quello di errore di inseguimento e(t) = w(t)-y(t), che ci dice di quanto la nostra uscita si discosta dall'andamento ideale voluto.Vogliamo che questo valore sia il più basso possibile e che le variabili controllate seguano quindi il più possibile il segnale di riferimento(andamento voluto).

Definizione: L'attuatore è quel componente che è connesso al controllore e consente appunto di controllare il sistema, quindi nel caso del cruise control, sarà l'acceleratore per noi.

Il primo problema che si presenta adesso è quello di scrivere il nostro sistema di cruise control sotto forma di modello matematico, come visto di sopra. Il nostro obbiettivo è adesso scrivere le equazioni di stato e la trasformazione d'uscita(come visto prima) della macchina, quindi del nostro sistema, perchè è proprio dal modello matematico del sistema che si può progettare il controllore, senza non si può!

Quindi la prima cosa è scrivere il modello del sistema:

1- Scegliamo l'input u(t) e l'output y(t). Non c'è una scelta giusta e una sbagliata, ma ovviamente nel nostro caso viene spontaneo dire che l'ingresso sarà la pressione sul pedale(la chiamo quindi u(t)) e come uscita y(t) scegliamo la velocità del veicolo v(t).

2- Bisogna adesso scegliere lo stato, cioè l' insieme di variabili che riassumono tutte le informazioni necessarie per descrivere completamente l'evoluzione futura del sistema,rappresenta la "memoria" del sistema in un certo istante, determinando come si comporterà successivamente.
In questo caso vediamo subito che la velocità basta come unico stato perchè da questa possiamo determinare l'andamento futuro del sistema dato un qualsiasi ingresso.
Ora scriviamo una relazione tra stato e ingresso. Scriviamo allora la forza totale considerando anche l'attrito che agisce sulla macchina: Fr sarà per noi la resistenza aerodinamica e l'attrito,che supponiamo valere Fr = c_r * v(t), dove c_r è una costante. Questa espressione è una buona approssimazione per il nostro studio,ma possiamo utilizzare anche approssimazioni più precise e complesse.


Dobbiamo adesso trovare un modo di passare dalle forze alle velocità. Diremo innanzitutto che la forza totale sulla macchina sarà F = u(t)-Fr(t). Ora, sappiamo che una forza per la seconda legge di Newton è una massa per una accelerazione e che l'accelerazione non è altro che la derivata della velocità rispetto al tempo(cioè la variazione di velocità diviso un lasso di tempo infinitesimo in cui essa avviene), quindi otteniamo una equazione differenziale:



nella prima riga si vede come abbiamo applicato la seconda legge di Newton e infatti abbiamo scritto l'accelerazione come derivata della velocità, moltiplicata per la massa della macchina.
Questo era ovviamente un caso banale, di un sistema del primo ordine(l'ordine è il numero di stati).Di solito c'è sempre più di un solo stato, quindi si trovano più equazioni differenziali con x_1,x_2 ecc...

Come possiamo notare, i coefficienti nelle espressioni dipendono sempre da x e da u, in più questi coefficienti sono anche delle costanti, quindi il sistema si dice lineare.Infatti i sistemi con questa caratteristica possono essere semplificati e scritti in forma matriciale(se non sai cos'è una matrice ti consiglio di vedere l'argomento, se invece non ricordi bene come si usano, puoi guardare le prime tre pagine del riassunto che ho caricato all'inizio della pagina):



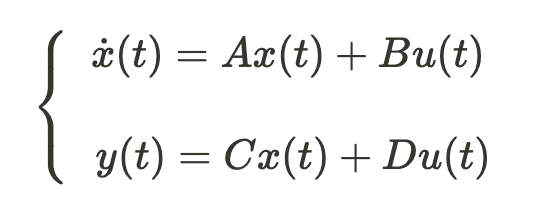
Dove A è la matrice dei coefficienti degli stati(nel nostro caso era un numero perchè avevamo un solo stato x che era la velocità),questa matrice è detta matrice della dinamica, poi vedremo il perchè,inoltre è una matrice quadrata. Poi c'è la matrice B che invece lega i coefficienti degli ingressi con la derivata dello stato, è un vettore. Poi c'è C che è di tipo riga e sono i coefficienti dello stato sulla trasformazione di uscita(nel nostro caso valeva 1,era sempre un numero perchè lo stato era uno solo).Infine c'è D che è la matrice dei disturbi e lega gli ingressi con l'uscita.



come si può vedere, in un sistema con 2 stati si ha una matrice A 2x2 che rappresenta i coefficienti di x1 e x2.La prima riga della matrice rappresenta i coefficienti(sui termini x1 e x2) nell'equazione differenziale di x1,la seconda quelli dell'equazione differenziale di x2.

Come classificare un sistema? Dato un sistema nella forma che abbiamo visto (con le equazioni differenziali degli stati e la trasformazione d'uscita), è molto semplice:

1) Lineare? per dirlo basta guardare i coefficienti di u(t) e di x(t) nelle equazioni del sistema(quindi sia stato che uscita), se sono tutte costanti allora è lineare, altrimenti non lo è(ad esempio se c'è un esponenziale).

2) Stazionario o Tempo Variante ? Ancora, si guardano i coefficienti di u(t) e di x(t) e se i coefficienti non dipendono dal tempo allora il sistema si dirà stazionario, altrimenti tempo variante.

3) Dinamico o Statico ? Se c'è almeno 1 equazione differenziale sarà dinamico, altrimenti se non c'è uno stato(perchè non sempre serve) il sistema è Statico

4)Proprio strettamente o Proprio, non strettamente ? se l'input non compare nell'equazione di uscita (quindi D=0) allora il sistema è proprio strettamente.

5)SISO,MISO,MIMO,SIMO? S=Single M=Multiple I = Input O = Output: se l'input è un vettore anzichè un numero sarà Multiple Input altrimenti Single Input, idem per l'output... Il nostro cruise control è SISO perchè c'è un solo input e una sola uscita(se c'erano y1(t)=... y2(t)=... quello non era Single Output)

Stabilità e Equilibrio Sitemi

Equilibrio: condizione nella quale le variabili di stato del sistema non variano nel tempo, ovvero il sistema non evolve ulteriormente. Matematicamente si traduce in una condizione molto semplice. Se il sistema è a tempo discreto, cioè la variabile tempo non è t appartenente ai reali, ma il tempo del sistema sarà campionato, frazionato cioè in istanti, che possono essere mesi, minuti ecc...
Un sistema a tempo discreto è un sistema in cui le variabili di stato e gli input sono aggiornati a intervalli di tempo discreti, ossia il tempo avanza in passi distinti (ad esempio, t = 0, 1, 2, ...).
Infatti al posto della derivata di x(t) ci sarà semplicemente x(k+1) = ... come equazione di stato, k+1 proprio per indicare che ci si riferisce all'istante successivo.

Quando si deve studiare un sistema su un computer, ad esempio quando si parla di sensori, non possiamo rappresentare il tempo come variabile continua, per un computer ci sono solo istanti discreti perchè la memoria è in quantità finita e servirebbe infinita memoria per rappresentare il tempo come continuo. Da qui infatti si potrebbe fare un discorso sul campionamento, che evito per non appesantire la spiegazione già complessa.In breve, quando si campiona un segnale, c'è un trade off tra il numero di campioni e la qualità del segnale che si ottiene(meno campioni = meno informazione ma anche meno memoria e prestazioni usate).

Tornando all'equilibrio(cioè la condizione in cui il sistema è "fermo", cioè non evolve lo stato) si hanno le seguenti condizioni:

-x(k+1) = x(k);condizione di equilibrio se il sistema è a tempo discreto

-ẋ(t) = 0 (derivata si anulla); condizione di equilibrio se il sistema è a tempo continuo

Nel caso del nostro cruise control, l'equilibrio c'è quando la velocità diventa costante e quindi le forze si bilanciano, infatti la derivata dello stato sarà nulla. L'equilibrio avviene a seguito di un certo ingresso dato al sistema, infatti spesso negli esercizi si richiede proprio di trovare l'ingresso o gli stati per cui si verifica questa condizione. Per trovarli, le condizioni da imporre sono quelle scritte di sopra, in base al fatto che il sistema sia a tempo continuo o discreto.

Un equilibrio può avere una caratteristica particolre,quello di essere asintoticamente stabile:



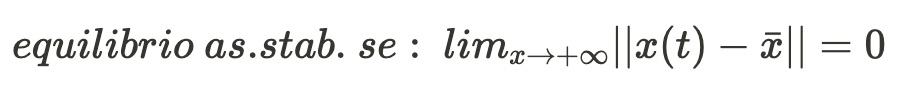
il che vuol dire che quando il sistema si trova in questo stato di equilibrio che ha questa caratteristica, se viene leggermente perturbato da questo punto di equilibrio, il sistema tenderà a tornare proprio all'equilibrio, convergendo proprio al punto di equilibrio.
Per perturbazione si intende è una piccola variazione o deviazione temporanea dallo stato di equilibrio di un sistema. È un cambiamento esterno o interno che sposta il sistema dal suo punto di equilibrio, qualcosa che disturba il sistema dal suo comportamento naturale.

C'è invece un'altra condizione fondamentale, molto più forte, che è quella di asintotica stabilità per il sitema e non solo degli equilibri: dire che un equilibrio è as. stabile non significa che il sistema convergerà a quell'equilibrio per qualsiasi valore di ingresso e stato, ma solo per particolari valori.
Il fatto di convergere è una cosa molto importante, perchè se diverge vuol dire che si comporta in maniera anomala,in un circuito elettrico ad esempio in cui l'uscita è una corrente, il fatto che diverge(va a infinito) vuol dire che qualche componente verrà danneggiato per esempio .

Quando invece diciamo che un sistema è asintoticamente stabile stiamo dicendo che per qualsiasi ingresso e stato il sistema a transitorio esaurito(dopo un tempo sufficientemente lungo, infinito per esprimere la condizione in matematica) converge ad un certo valore. Ad esempio, nel cruise control, all'inizio dobbiamo raggiungere la velocità voluta, quindi ci mettiamo diversi secondi a raggiungere la stabilità, supponiamo di dover arrivare a 150, partiamo da 50...all'inizio potrebbe essere necessario scalare la marcia e magari la velocità scenderebbe un po' inizialmente(sottoelongazione), per poi crescere e magari arrivare a un valore leggermente più alto, a.e. 156 (sovraelongazione) per poi stabilizzarsi a 150.



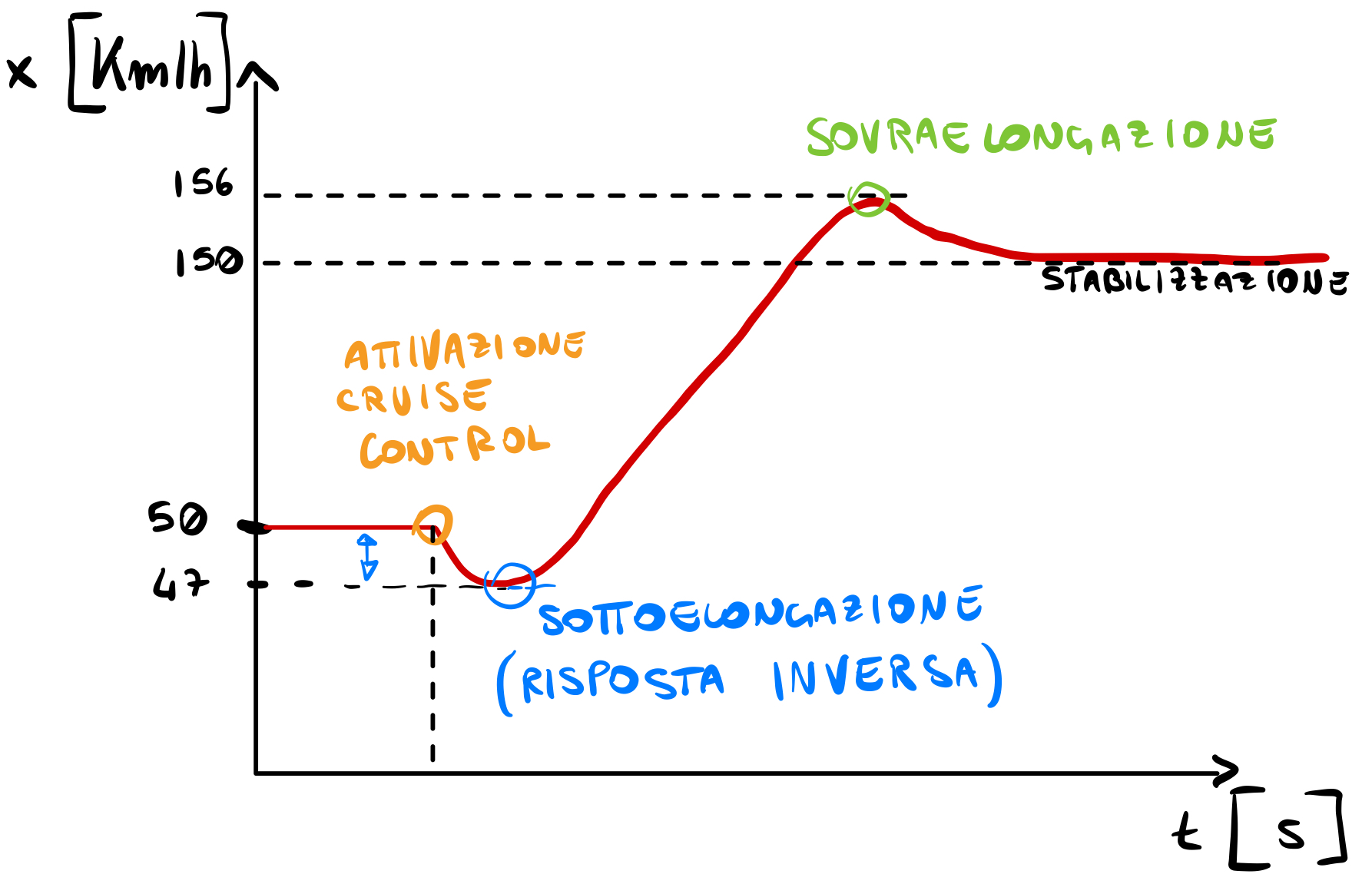
Ai più attenti sorgerà spontanea una domanda, come faccio a sapere se un sistema è asintoticamente stabile?
Fortunatamente se il sistema è lineare è molto semplice saperlo.Basta calcolare gli autovalori della matrice A vista prima(la matrice della dinamica).Una volta calcolati, procediamo cosi:

-Se il sistema è a tempo continuo la condizione per avere asintotica stabilità è che tutti gli autovalori abbiano parte reale negativa.Se anche uno solo è nullo, non possiamo dire nulla sulla as. stab. Ma, perchè proprio minore di 0 ?
Il motivo è semplice: tutti i sistemi lineari hanno una risposta(uscita nel tempo) che è sempre nella forma ⍺*e^(λt)+... dove alpha è un coefficiente,λ un autovalore e t il tempo. Da qui notiamo che se t tende a infinito e l'autovalore è negativo, questo termine viene portato a zero.Siccome l'uscita di un sistema lineare a tempo continuo è sempre fatta in questo modo, come somme di questi termini, se tutti gli autovalori sono negativi, il sistema converge sempre, cioè è asintoticamente stabile.nb: con la notazione ^ si intende che ciò che segue è a esponente.

-Se il sistema è a tempo discreto la condizione è che tutti gli autovalori abbiano modulo minore di uno, cioè -1 < λ < +1. Questo perchè la risposta nei sistemi lineari a tempo discreto è nella forma y(k) = ⍺*λ^k + ... Quindi se il modulo è minore di 1 è ovvio che la somma di termini di quel tipo per k->+∞ convergerà. Quidni il sistema sarà as. stab.

Se ci viene chiesto di calcolare il movimento libero o risposta libera(cioè quando l'ingresso è nullo,u(t)=0), faremo in entrambi i casi cosi: prima calcoliamo gli autovalori, poi imponiamo due condizioni per ottenere un sistema a due equazioni, cioè sicuramente conosciamo(o ci viene data) y(0), a quel punto ho la prima equazione, ad esempio, a tempo continuo y(0) = ae^-2t + be^-t , dove y(0) sarà un numero ovviamente(la cosa comoda è che con 0 rimane a+b=y(0)). Poi scrivo la seconda che potrebbe essere y(1) = ... e cosi arrivo a un semplice sistema di due equazioni e posso calcolare i due coefficienti a e b. Cosi ho scritto l'equazione della risposta libera...

Sistemi Lineari

Abbiamo visto che un sistema lineare è un modello molto semplice e ci permette di studiare in modo altrettanto semplice l'asintotica stabilità. Tuttavia, calcolare la risposta ad un ingresso generico può essere molto complesso.Prima abbiamo calcolato il movimento libero che è l'uscita y(t) in assenza di ingressi, u(t) = 0. Quando invece il movimento è forzato, quindi quando è presente un ingresso, calcolare direttamente y(t) è molto complicato, perchè bisogna risolvere un integrale con le matrici A,B,C,D:



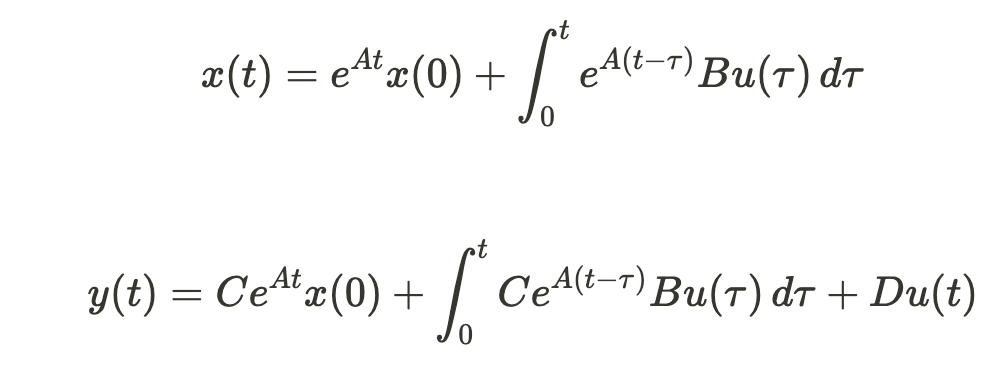
Questa era la Formula di LaGrange.Noi invece utilizzeremo un'altra strategia, che è la Funzione di Trasferimento e l'antitrasformata dal dominio di Laplace(dal dominio delle frequenze torneremo al tempo), ma vedremo in seguito cosa vuol dire. Spesso però i sistemi non sono lineari, sono molto complicati, però possiamo semplificarli e linearizzarli.Questo ovviamente porta a fare un'approssimazione che per alcuni sistemi può risultare ottima e per altri pessima, dipende dal tipo di sistema.
Come si linearizza un sistema ? Vediamolo da un esempio, ho un certo sistema di partenza che presenta termini quadratici ad esempio e voglio farlo diventare lineare... Chiaramente questo si può fare solo intorno ad uno specifico punto, infatti si parla di linearizzazione attorno a un punto.Quello che si fa è prendere la matrice dei coefficienti, trovare la derivata(per le matrici A e C rispetto agli stati x, per B e D rispetto agli ingressi u) e poi calcolare il valore della derivata in quel punto(attorno a un certo stato x e un certo ingresso u quindi):





abbiamo cosi ottenuto il sistema linearizzato attorno a un punto.Quella che si vede all'inizio è la linearizzazione di un sistema generico.

Funzione di Trasferimento,Risposta in Frequenza

In molti ambiti dell'ingegneria e dell'automazione è utile cambiare dominio, passare dal dominio del tempo a quello delle frequenze, perchè semplifica di molto lo studio dei sistemi e permette infatti di semplificare di molto i calcoli, ad esempio, una derivata nel dominio di Laplace(cioè delle frequenze, dopo vediamo perchè Laplace), è una semplicissima differenza, un integrale diventa una divisione ecc...

Invece di osservare il segnale direttamente nel tempo, analizzi quali frequenze sono presenti nel segnale e come ciascuna frequenza contribuisce al segnale complessivo. Questo risulta particolarmente utile perchè spesso i segnali sono sinusoidali.Usiamo la trasformata di Laplace per passare al dominio delle frequenze:



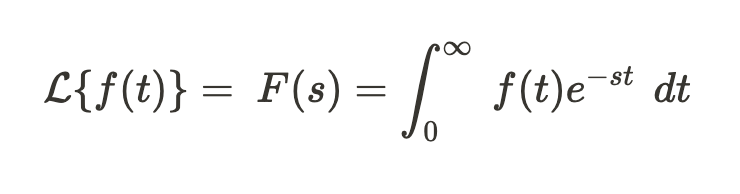
dove f(t) è la funzione nel dominio del tempo che si vuole trasformare per passare al dominio delle frequenze, F(s) è la funzione trasformata.
Da notare il cambio di variabile nella nuova funzione, da t ad s, s è un numero complesso in realtà, quindi un numero che si rappresenta sul piano di Gauss con una parte Reale e una Immaginaria s = Re(s) + j* Im(s).

Se non conosci i numeri complessi, le operazioni in questo dominio ecc... ti consiglio di studiare prima l'argomento perchè necessario per affrontare questa parte.

Nella maggior parte dei casi non ci toccherà utilizzare questo integrale perchè in realtà ci sono una serie di regole di trasformazione, per passare da una funzione che è nel dominio del tempo ad una nel dominio delle frequenze. L'operazione di trasformazione si indica con L{f(t)} dove L sta per Laplace, f(t) è la funzione da trasformare.
Ecco un tabella che ho preparato per trasformare una funzione dal dominio del tempo al dominio di Laplace velocemente:



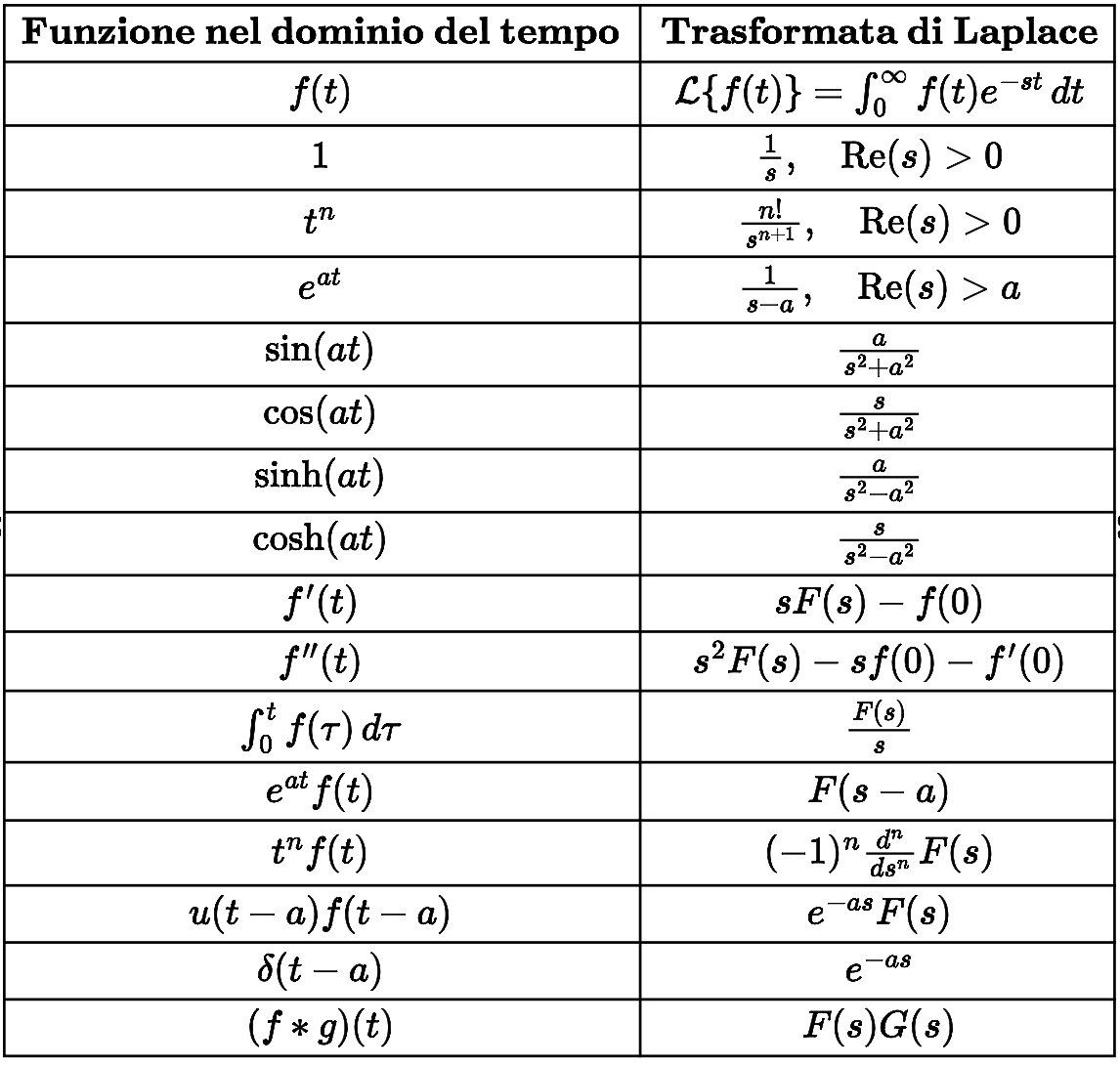
Puoi usare questa tabella per trasformare la maggior parte delle funzioni, come si può notare è molto semplice utilizzarla, perchè basta prendere a sinistra la funzione nel dominio del tempo, a destra avremo il risultato della trasformazione. Ad esempio, se devo trasformare la costante 5, avrò 5/s (seconda riga, vale per qualsiasi costante).

Ci sono inoltre degli ingressi standard che sono molto utilizzati nei sistemi, ingressi realizzabili in modo relativamente facile in pratica e sono funzioni fatte nel seguente modo:



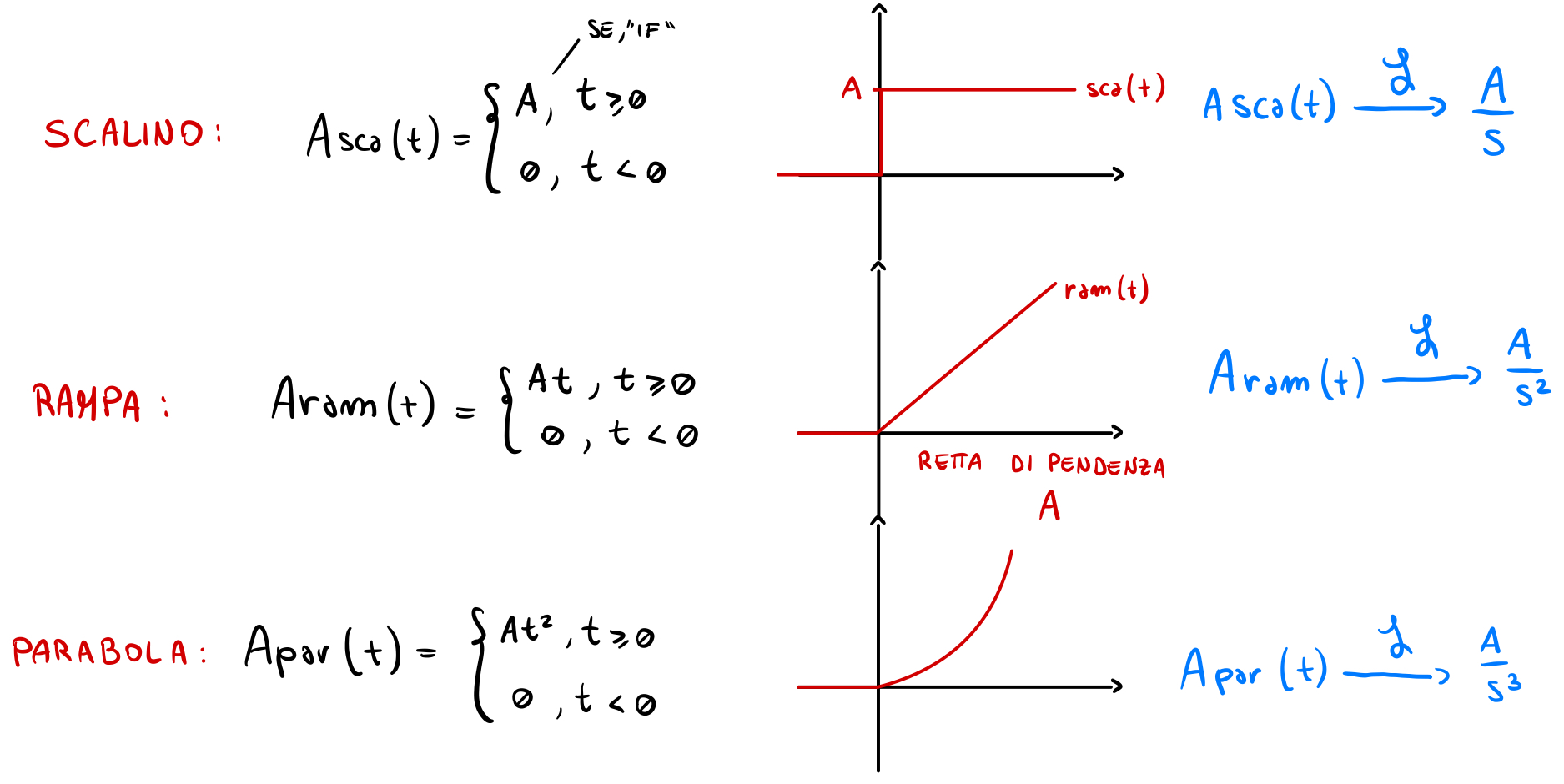
Ora introduciamo un concetto importante, quello di Funzione di Trasferimento(FdT) G(s).Lo scopo è sempre quello di rendere facile lo studio dei sistemi, e da qui in avanti scriveremo un sistema sempre con la sua funzione di trasferimento. La FdT è una funzione in Laplace che mette in relazione ingresso e uscita del sistema.Si presenta sempre nella forma di una semplice frazione, ad esempio 1/s * (s-1)/(s+2). Da questa semplice frazione possiamo ricavare informazioni importanti del sistema.



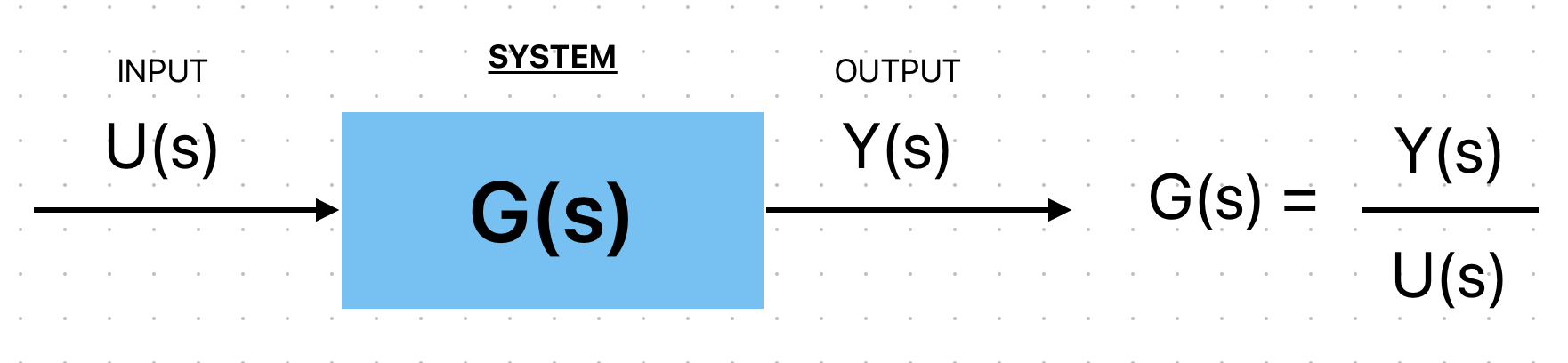
Quindi con 3 semplicissime funzioni, G,Y,U possiamo studiare l'intero sistema e in un dominio che rende il tutto ancora più facile.Per passare da funzione di trasferimento a dominio del tempo con la risposta anche del sistema basta ricondurci alle trasformate elementari viste nella tabella. Quindi G(s) è un modo di rappresentare il sistema, descrive la relazione che c'è tra ingresso e uscita.
Ecco un esempio di come si ripassa al dominio del tempo, calcolando una risposta a un ingresso U di tipo scalino:



(nb: si dovrebbe moltiplicare per l'ingresso anche all'inizio, dove facciamo A/... + B/..., li si doveva aggiungere C/s)

Abbiamo parlato della FdT, ma non di come si ottiene analiticamente, cioè dato il nostro sistema nella forma vista all'inizio(con le due espressioni di x derivato e y(t)), come ricavare la sua FdT ? Da qui si capirà il vero significato della FdT, ecco i passaggi...



Da qui si vede proprio come diventa semplice studiare la risposta di un sistema e capire subito la sua uscita. G(s) è una funzione che incorpora tutte le caratteristiche del sistema. Vediamo adesso il significato.

•Poli:matematicamente coincidono con gli autovalori della matrice A e sono quei valori che annullano il denominatore di G(s).Nell'esempio precedente c'erano due poli negativi(e quindi che danno stabilità asintonica,ricordiamo sempre questo) in s=-3 e s=-5. Un altro concetto molto importante in automatica è quello di costante di tempo che è una costante tipica di ogni sistema che fornisce una misura della velocità di risposta di un sistema dinamico a una variazione di ingresso.La costante di tempo di un sistema è il reciproco del polo che ha il valore più basso(per una approssimazione detta a polo dominante). Il più basso perchè chiaramente se è più basso il valore il reciproco si alza: es. 1/2 > 1/30...

•Zeri:coincidono con i valori che annullano il numeratore di G(s).Hanno un effetto rilevante quando il loro valore è inferiore a quello dei poli: se ho (s+2)/(s+30), lo zero 2 è dominante rispetto ai poli e quindi ha effetto rilevante. Per vedere qual'è l'effetto dobbiamo considerare il segno dello zero. Se lo zero è negativo(come nell'esempio fatto, s = -2), allora l'effetto sarà quello di una sovraelongazione, mentre se lo zero è positivo(ad esempio s-5), l'effetto sarà quello di una risposta inversa.

•Tempo di assestamento: facendo una approssimazione, possiamo dire che i sistemi lineari che stiamo studiando, esauriscono il transitorio dopo 5 costanti di tempo. Questo, è detto tempo di assestamento(nel nostro caso al 99,3%, cioè che dopo 5 costanti di tempo il transitorio è arrivato a quella percentuale e si è praticamente esaurito). Ricordo che il transitorio è transitorio è la fase temporanea che un sistema dinamico attraversa quando subisce un cambiamento nell'ingresso (come un gradino o un impulso) fino a raggiungere una nuova condizione di regime stazionario.

Inoltre è sempre bene tener presente che autovalori positivi e quindi poli positivi renderebbero il sistema instabile e quindi a tempo infinito divergerebbe come già spiegato.

C'è poi un'ultima considerazione da fare, cioè il caso in cui i poli siano complessi coniugati, e quindi il sistema presenti delle oscillazioni.



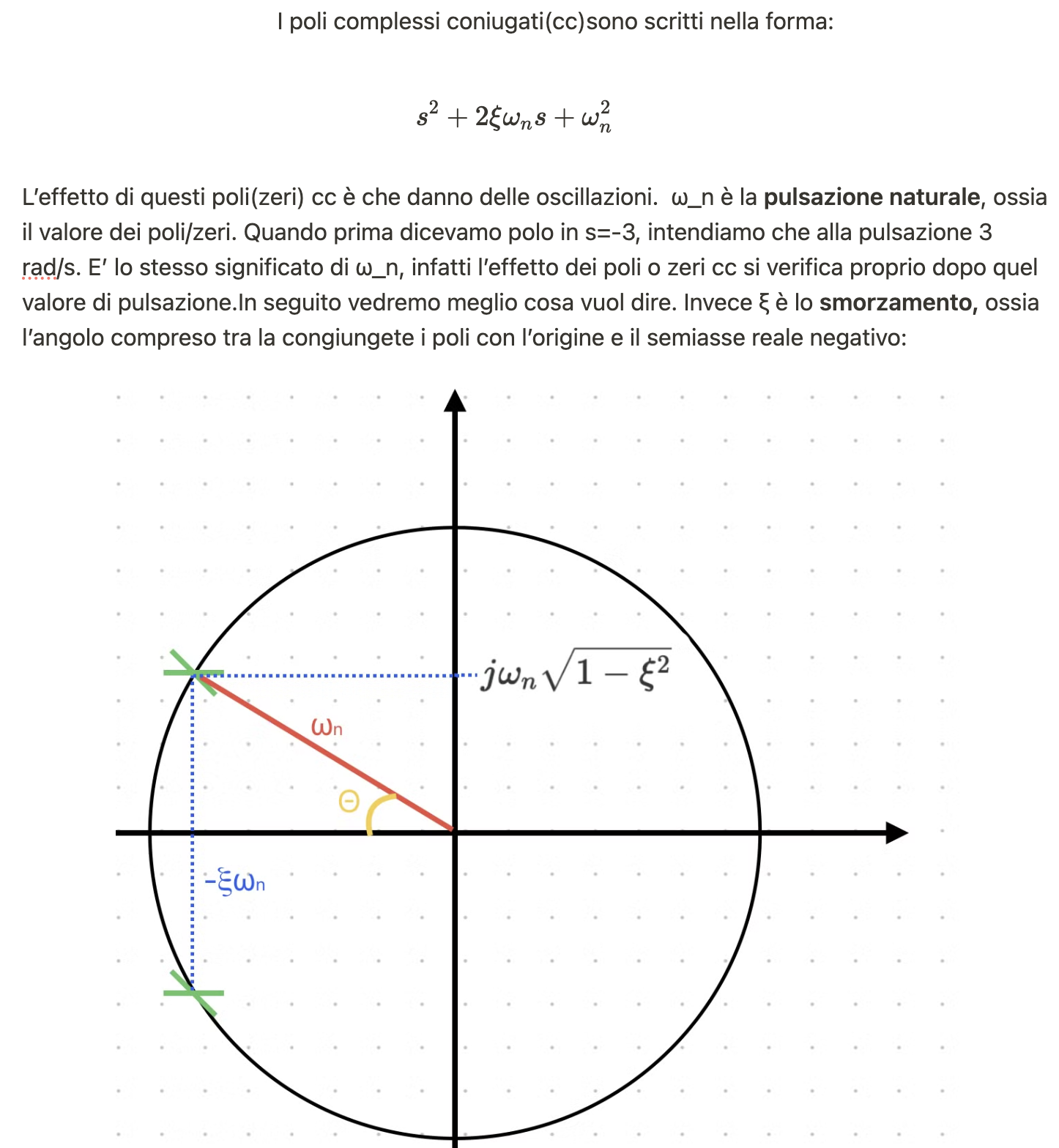
Inoltre, ξ è sempre compreso nell'intervallo [-1,1]:

• ξ < 0 implica oscillazioni divergenti(sistema non as. stab.)

• ξ > 0 vuol dire invece oscillazioni che convergono e quindi via via vanno ad annullarsi(dopo un po' il sistema non oscilla più)

• ξ = 0 significa oscillazioni costanti, non divergono ma non convergono e quindi continuano all'infinito(parliamo di oscillazioni in y(t))

Introduciamo adesso un altro concetto fondamentale, il guadagno statico μ. Il guadagno statico è un parametro che descrive il rapporto tra l'uscita e l'ingresso di un sistema quando quest'ultimo raggiunge una condizione di regime, ovvero quando tutte le variabili del sistema sono stabili e non più dipendenti dal tempo (situazione stazionaria, esaurito il transitorio,sarà il valore che assumerà quindi y(t) per t grandi, approssimativamente, dopo 5 volte la costante di tempo,indicata con T). Questo si ottiene facendo il limite di G(s) per s che tende a infinito, togliendo a G(s) tutti i poli e gli zeri presenti nell'origine.

A tal proposito, vale la pena spiegare l'effetto di poli e zeri nell'origine. Un polo nell'origine forma un cosiddetto integratore,significa che la risposta del sistema all'ingresso sarà proporzionale all'integrale dell'ingresso nel tempo. In altre parole, se l'ingresso è un passo (un valore costante), l'uscita continuerà a crescere indefinitamente.
Invece uno zero nell'origine costituisce un sistema detto derivatore:l'uscita del sistema è proporzionale alla derivata dell'ingresso nel tempo. Se l'ingresso cambia, l'uscita risponderà a questo cambiamento, ma se l'ingresso è costante, l'uscita rimarrà zero.Non introduce instabilità. Un polo nell'origine al contrario, non introduce stabilità in senso stretto, ma indica una crescita dell'uscita nel tempo, che può portare a un comportamento non controllato.

Facciamo inoltre una precisazione su un concetto già visto, il tempo di assestamento.Abbiamo parlato di quello al 93%, ma in generale, il tempo di assestamento è il tempo necessario perchè il modulo della differenza tra l'uscita e il valore di regime rimanga sotto al ε% (ecco cosa significa dire tempo di assestamento al 1% ad esempio, 1%=ε).

Infine, un'informazione esplicita nella G(s) è il fatto di essere strettamente propria o meno: se il numero di poli è strettamente maggiore del numero di zeri, avremo una G(s) strettamente propria.

Schemi a Blocchi, Raggiungibilità, Osservabilità

Nella pratica conviene spesso rappresentare sistemi lineari stazionari che sono costituiti da più sottosistemi, con gli schemi a blocchi. In questa rappresentazione una variabile è rappresentata da una freccia, un sistema è rappresentato da un rettangolo(blocco),al cui interno è scritta la funzione di trasferimento(perchè appunto la FdT è la relazione ingresso-uscita).



Ora però introduciamo altri componenti essenziali: il nodo sommatore e il punto di diramazione.
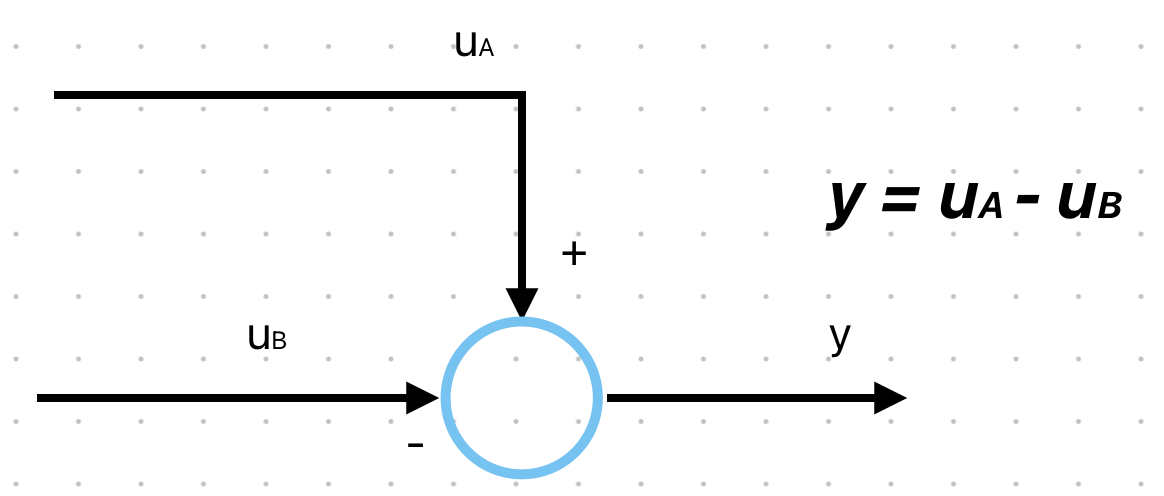
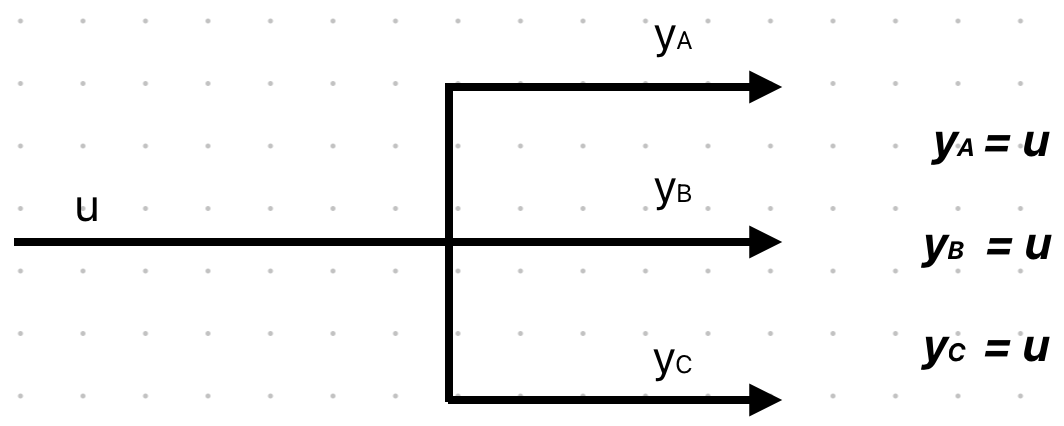
Il nodo sommatore si indica con un cerchio ed effettua la somma algebrica delle variabili che entrano al suo interno e porta quindi la somma in uscita. Ogni variabile che entra ha segno + o - (infatti può fare anche una sottrazione di segnali oltre che addizione).Il punto di diramazione invece duplica la variabile di ingresso e la riproduce identica in uscita. Vediamo entrambi i componenti rappresentati:

nodo sommatore:


punto di diramazione:


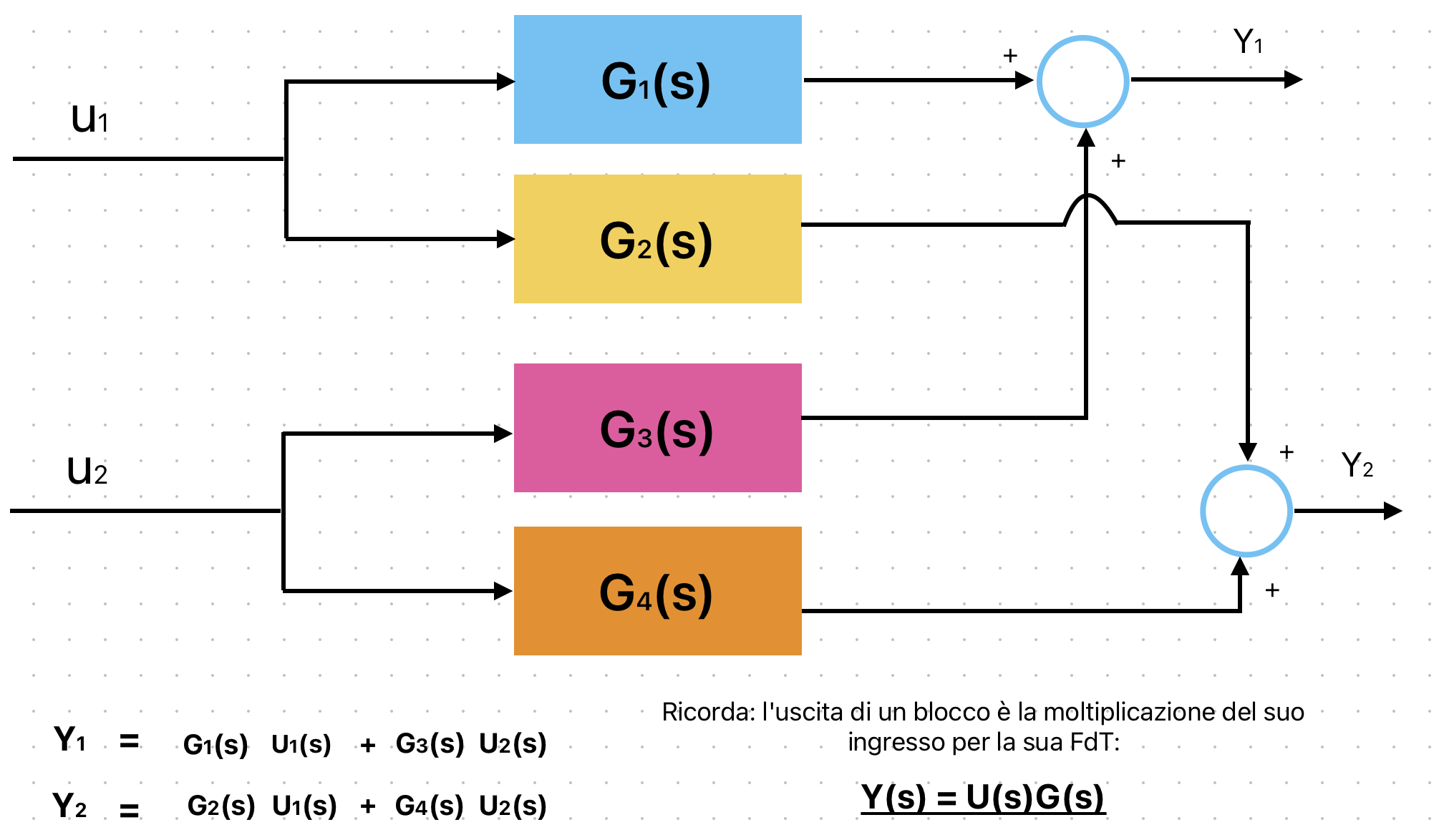
Ho preparato un esempio con 4 sistemi connessi, 4 ingressi e 2 uscite. Cerchiamo di capire come si ottengono le uscite Y1 e Y2.Capito questo, non avremo problemi con gli schemi a blocchi!


Le connessioni tra i blocchi possono essere di tre tipi: in parallelo, in serie, oppure in retroazione(che vedremo nel capitolo successivo). Ecco degli schemi per impararle velocemente:



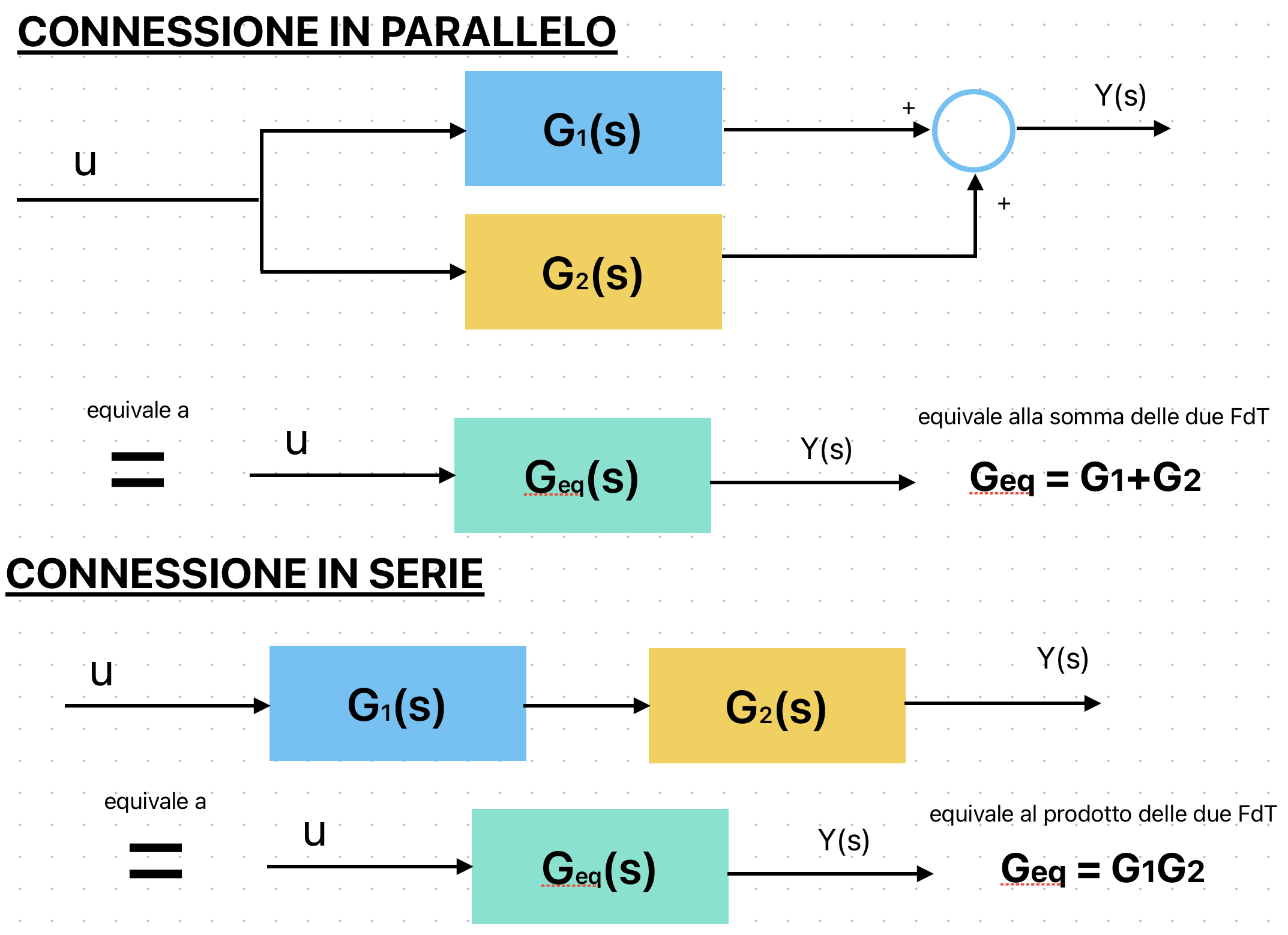
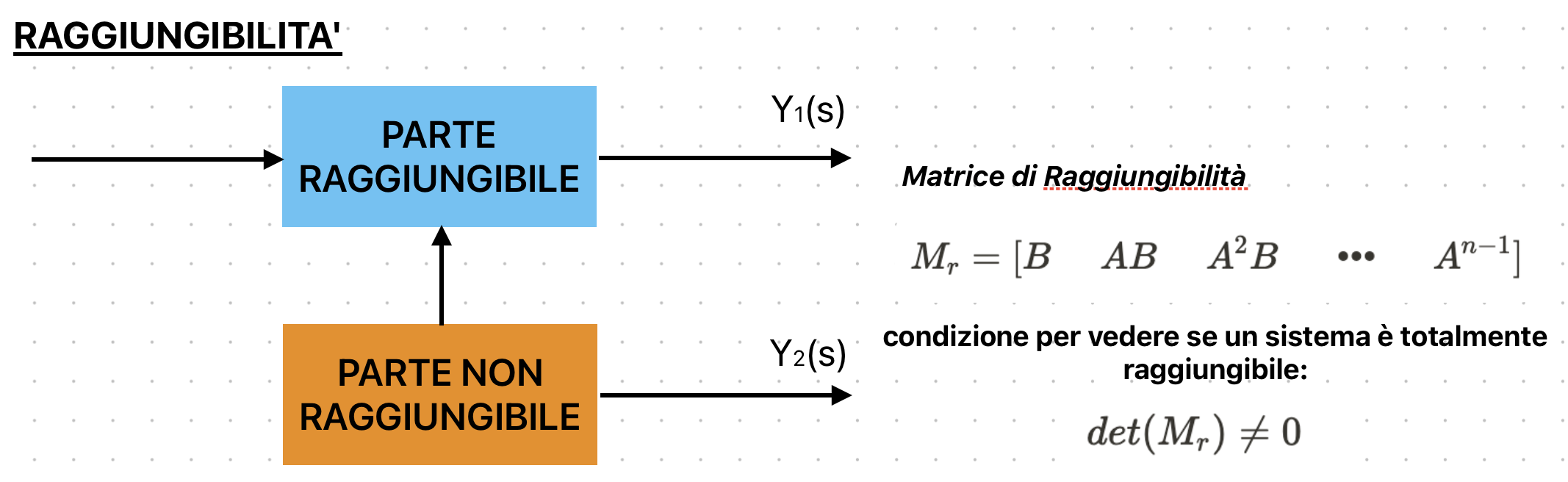
Per concludere con gli schemi a blocchi, mancano due concetti essenziali, che sono la Raggiungibilità e l'Osservabilità di un sistema.
Se un sistema ha una parte non raggiungibile vuol dire che ci sono state delle cancellazioni e quindi ci sono parti nascoste nel sistema, per cui se quella parte cancellata era instabile, nella FdT non la vedrò più e potrei erroneamente pensare che il sistema sia asintoticamente stabile. Dire che un sistema è completamente raggiungibile vuol dire che non ci sono state cancellazioni. Non raggiungibile vuol dire che l'input non riesce a influenzare lo stato di un blocco.



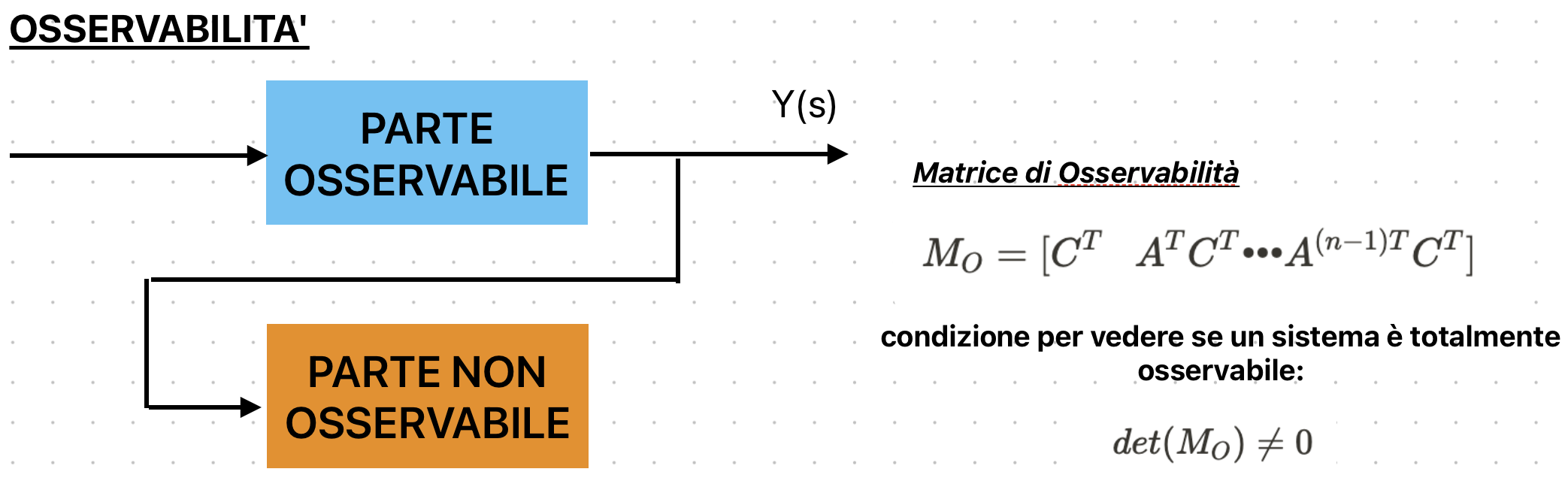
L'osservabilità invece è un concetto molto simile: un blocco è osservabile se quel blocco riesce a influenzare l'output del sistema complessivo.Vale il discorso fatto di sopra per le cancellazioni.Il sistema visto prima non era neanche osservabile, infatti c'erano due input separati.Per essere osservabile, nell'equazione del sistema(l'equazione nel tempo) e in particolare nella trasformazione d'uscita deve comparire anche y2(ad esempio y1 e y2 dovevano essere connesse con un nodo somma). Lo stesso vale per la raggiungibilità: nelle derivate degli stati deve comparire l'input(se ho due stati per esempio xA e xB, e su xA compare u, ma in xB no,ma compare xA, che a sua volta era influenzato da u, allora quello è raggiungibile, invece se non c'era neanche xA e quindi u non compariva per niente, non era raggiungibile).

Diagrammi di Bode e di Nyquist,Closed Loop e Criteri

Vediamo adesso cos'è la risposta in frequenza:supponiamo di avere un altoparlante e di voler sapere come risponde a diverse frequenze (bassi, medi, alti). La risposta in frequenza ti dice quanto l'uscita del sistema cambia in funzione della frequenza dell'ingresso(ad esempio se attenua le alte o le basse frequenze...). Un filtro passa-basso è un sistema che fa passare frequenze basse e taglia quelle alte, mentre un filtro passa-alto fa passare le alte frequenze e taglia quelle basse.

I due modi più usati per rappresentare la risposta in frequenza sono i diagrammi di Bode e di Nyquist. Partiamo da quelli di Bode.Noi disegneremo quelli asintotici, con semplici rette(quelli reali differiscono leggermente ma sono molto più complessi da disegnare). Ci sono due diagrammi di Bode che ci interessano, quello del modulo, sul cui asse orizzontale c'è la pulsazione ω e su quello verticale |G(jω)| cioè la FdT al variare delle frequenze,ci mostra il guadagno(quindi da qui vediamo se lascia passare le alte o le basse frequenze ad esempio) con j unità immaginaria.Il secondo che ci interessa è il diagramma della fase, che mostra il ritardo o l'anticipo con cui il segnale di uscita segue quello di ingresso, misurato in gradi. Un valore positivo della fase significa che l'uscita è in anticipo rispetto all'ingresso, mentre un valore negativo significa che l'uscita è in ritardo.Inoltre questo ci da un'indicazione sulla stabilità del sistema.

Come si disegnano ? Iniziamo da quello della fase: la prima cosa da vedere è il guadagno statico, che è quel valore di |G(jω)| quando ω = 1.Questo si vede facendo il limite per s->∞ di G(s) senza poli e zeri nell'origine. A questo punto passiamo sulla carta logaritmica per disegnarli e segnamo l'asse 0, dove preferiamo(se non si devono rappresentare valori troppo grandi o troppo piccoli sulle ordinate, va bene metterla al centro).Poi segnamo le decadi, cioè segnamo i valori sotto ad ogni tratteggiatura dove c'è lo spazio più ampio(come si può vedere si moltiplica per 10 ad ogni decade):



Posizioniamo inoltre anche i valori sulle ordinate, il primo è il diagramma del modulo, infatti si segna in scala Decibel(dB). Per passare |G(jω)| in dB basta fare 20*log₁₀(|G(jω)|), ad esempio se ho 0.1 da convertire faccio 20*log₁₀(|0.1|) = -20dB.
Quello mostrato è un modo molto comodo di piazzare i valori, ma se dovessero servire valori di pulsazione più alti o più bassi possiamo spostarlo come vogliamo.Idem per la fase, se dobbiamo arrivare a valori sotto -360, possiamo far partire l'asse dei zero gradi più in alto, in modo da avere più valori(idem per il modulo). Prendiamo adesso un sistema da rappresentare, quindi la sua FdT, e iniziamo a rappresentarla.Prendiamo ad esempio G(s) = -10 · 0.8 - s s(s + 2)(s + 10)

Come si può notare c'è un polo nell'origine(s=0), per cui dobbiamo fare qualche considerazione prima di iniziare a disegnare il diagramma del modulo. Quando ci sono poli nell'origine cambia la pendenza con cui si inizia a disegnare il modulo(da sinistra).Se c'è un solo polo, si inizia a pendenza -20dB/DEC, anche detta pendenza 1.Quindi iniziamo a tracciare una retta con quella pendenza(pendenza -20 vuol dire che tra una decade e l'altra, ad esempio parto da ω=0.1, parto da 40dB ad esempio e devo arrivare a ω=1 a 20 dB,guarda l'immagine che segue). Con due poli nell'origine si comincia a pendenza -40, tre -60 ecc... Come per ogni retta, ci servono due punti per iniziare a tracciarla e la tracceremo da destra verso sinistra, partendo da ω = 1 e come altezza si prende il guadagno statico, che per la nostra G(s) vale circa 0.07, cioè -23dB.Poi si torna indietro di una decade esatta(quindi ci posizioniamo a ω=0.1) e segnamo un punto a -3dB (siamo saliti di una decade,-23+20, 20 era la pendenza).



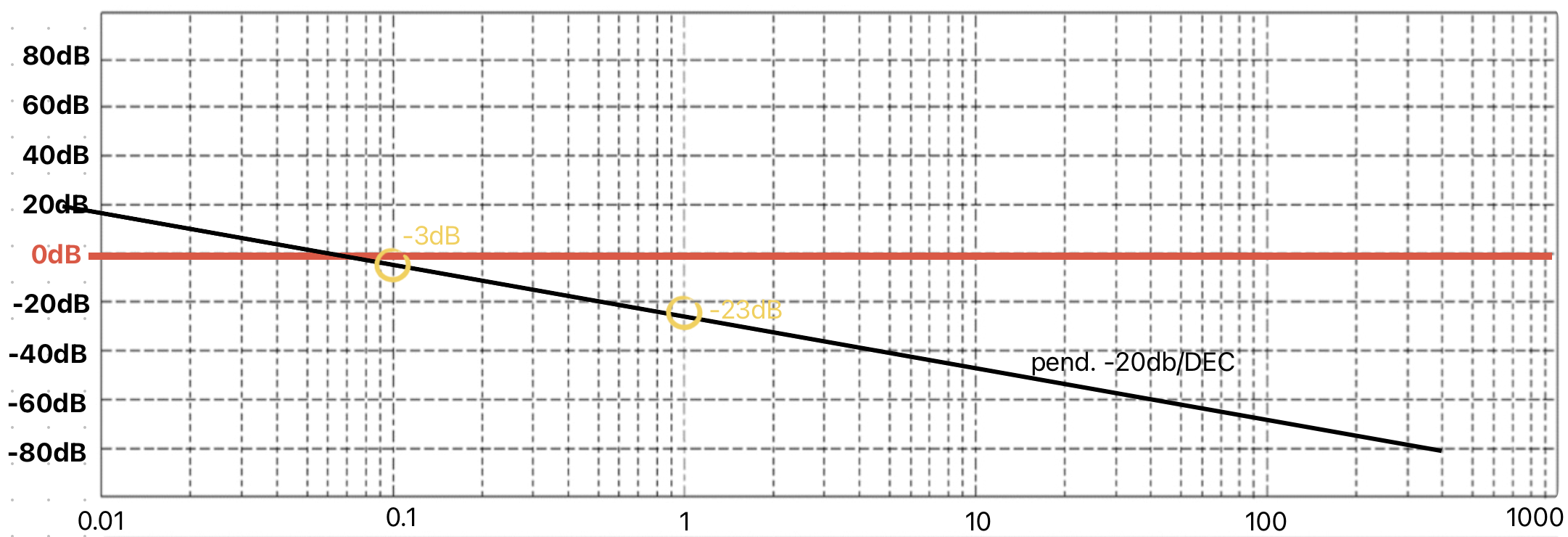
Questa era la parte "statica" del sistema, adesso però dobbiamo aggiungere la dinamica, quindi i poli e gli zeri del sistema. I poli abbassano la pendenza di -20(quindi dalla omega del polo in poi si abbassa di -20 la pendenza), mentre gli zeri la alzano di +20. Apportiamo quindi le modifiche, partendo da sinistra verso destra, modificando la retta già tracciata. Ovviamente, se non c'erano poli o zeri nell'origine, partivo da pendenza 0(retta orizzontale) con altezza pari al guadagno statico(-23dB).Applichiamo zeri e poli(segno con una X i poli e con un cerchio gli zeri):



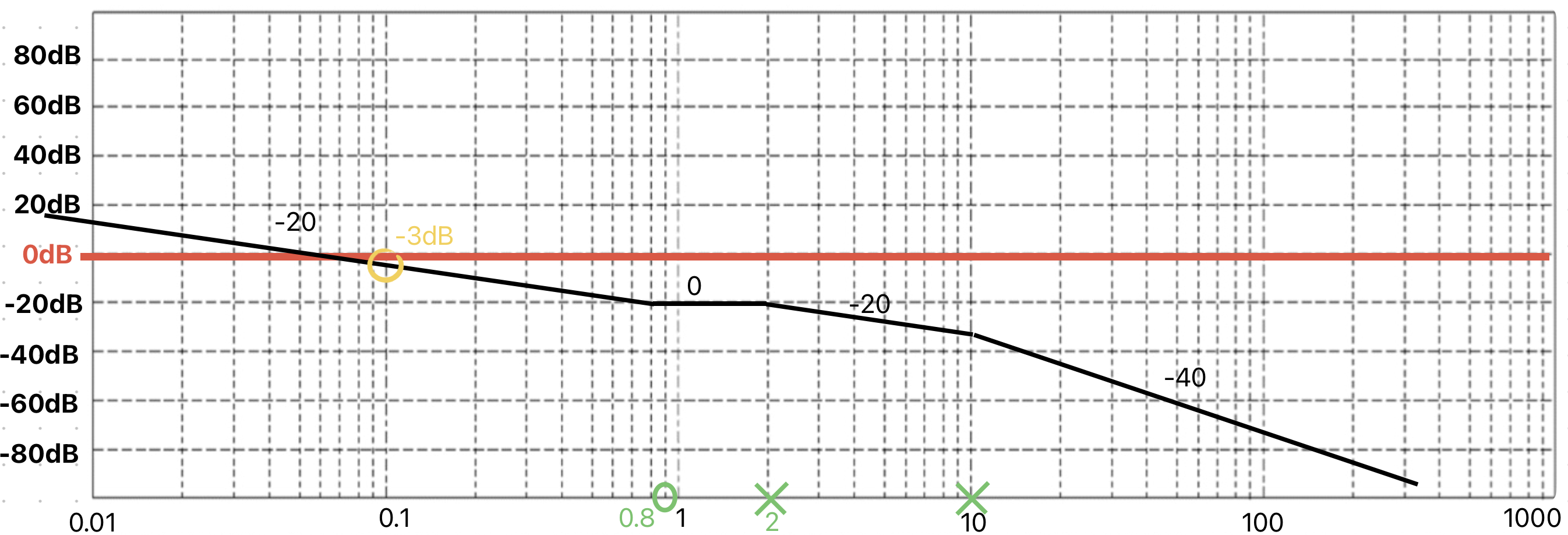
n.b : zeri: s=0.8; poli: s = -2, s = -10

Come si può vedere, partendo dalla retta disegnata prima abbiamo aggiunto il contributo di poli e zeri e abbiamo corretto le pendenze.

I più attenti si staranno chiedendo se cosi facendo non rispetterei più il guadagno statico: in ω = 1 non passo più in -23dB perchè lo zero in 0.8 mi ha cambiato la pendenza, ma questo non importa perchè l'importante è passarci quando non ci sono singolarità(poli e zeri), questa è una cosa che ci tornerà utile nel progetto del regolatore.
Il guadagno statico va tracciato sempre senza considerare poli e zeri non nell'origine.
Come si può notare lo zero in 0.8 mi ha fatto alzare la pendenza di +20, ma siccome era a -20, la pendenza risulta 0 dopo lo zero in ω = 0.8.

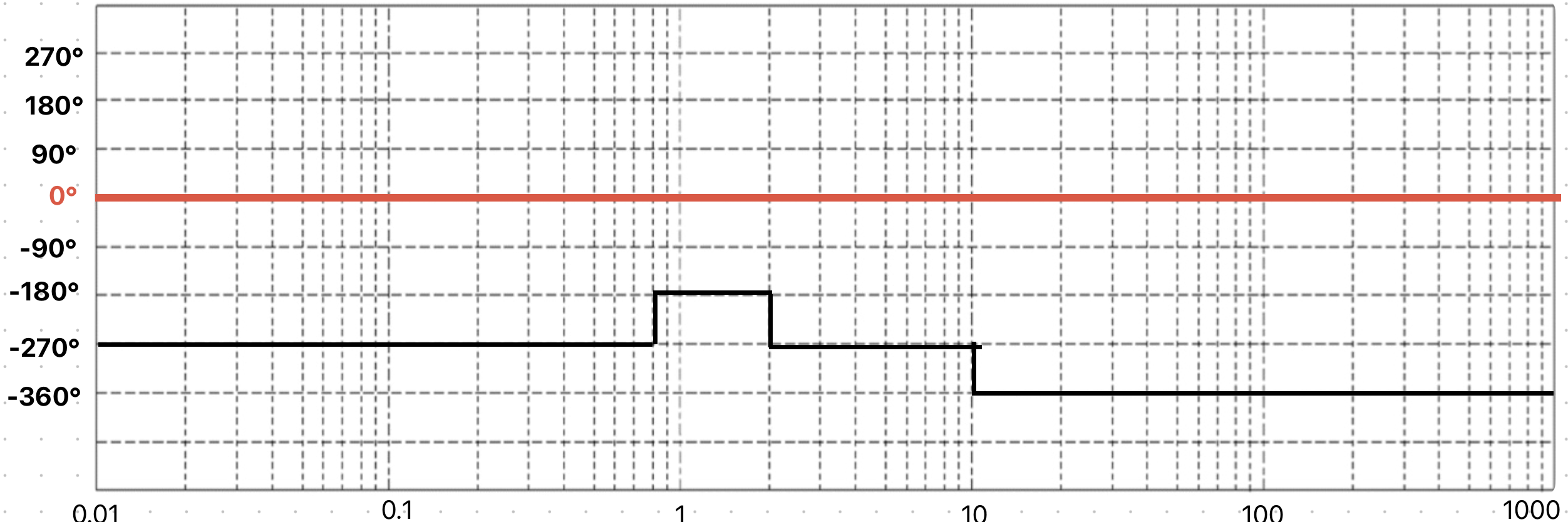
Il diagramma della fase è molto semplice da disegnare,infatti solo solo rette orizzontali, basta seguire queste regole:

•si parte da -180° se il guadagno statico è negativo, da 0 se positivo(non il valore in dB, ma quello risultante dal limite)

•oltre a questo valore, se sono presenti poli nell'origine scendiamo di ulteriori -90° * numero di poli nell'origine,al contrario si sale se sono poli nell'origine. Quindi se per esempio ho un guadagno negativo e 2 poli nell'origine devo iniziare da -180-(90*2) = 360.

•si inizia con una linea orizzontale e si procede fino alla prima singolarità.

Un polo negativo abbassa la fase di 90°, un polo positivo la alza di 90. Uno zero positivo la abbassa di 90°, uno zero negativo la alza di 90.

•definizione: pulsazione critica: indicata con ω_c, pulsazione alla quale |G(jω)| = 1, cioè la pulsazione alla quale il diagramma del modulo attraversa l'asse degli zero decibiel.Quella che si trova prima di questo valore è la banda passante.



Un altro tipo di diagramma che ci serve è quello di Nyquist. Per disegnarlo bisogna prima tracciare il Diagramma Polare e poi disegnare il suo simmetrico e l'insieme delle due figuare formerà il diagramma di Nyquist.

Il diagramma polare è la rappresentazione del sistema sul piano di Gauss.Si parte da ω=0, vedo quindi dal diagramma di Bode del modulo quanto vale G(jω).A questo punto vedo l'angolo dal diagramma della fase.L'angolo segnato è l'angolo preso a partire dal semiasse reale positivo in senso orario.Poi faccio scorrere ω fino a infinito.



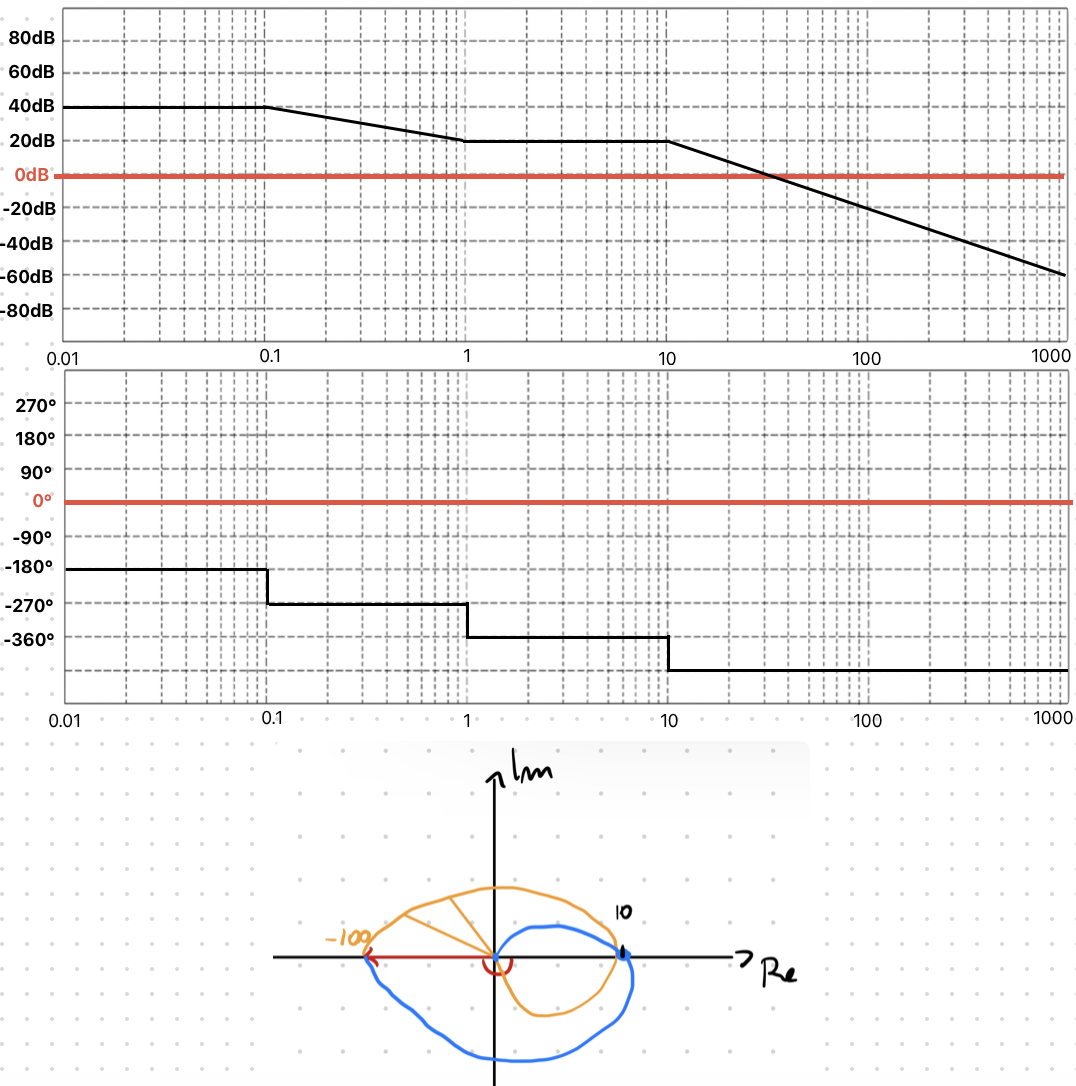
Prima di vedere il progetto, dobbiamo affrontare questi argomenti: Retroazione, funzione di Sensitività, Sensitività Complementare, criterio di Bode e di Nyquist.



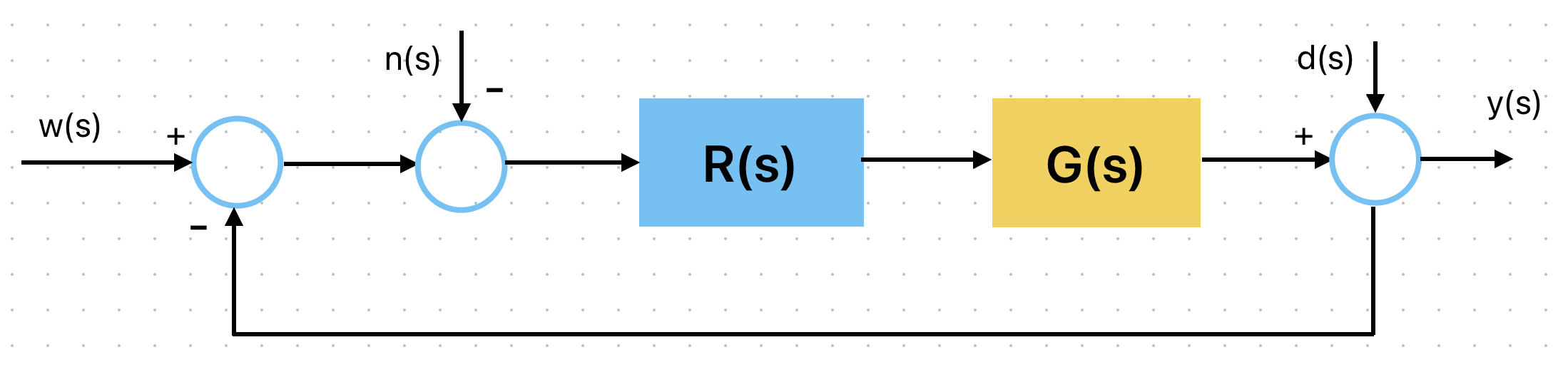
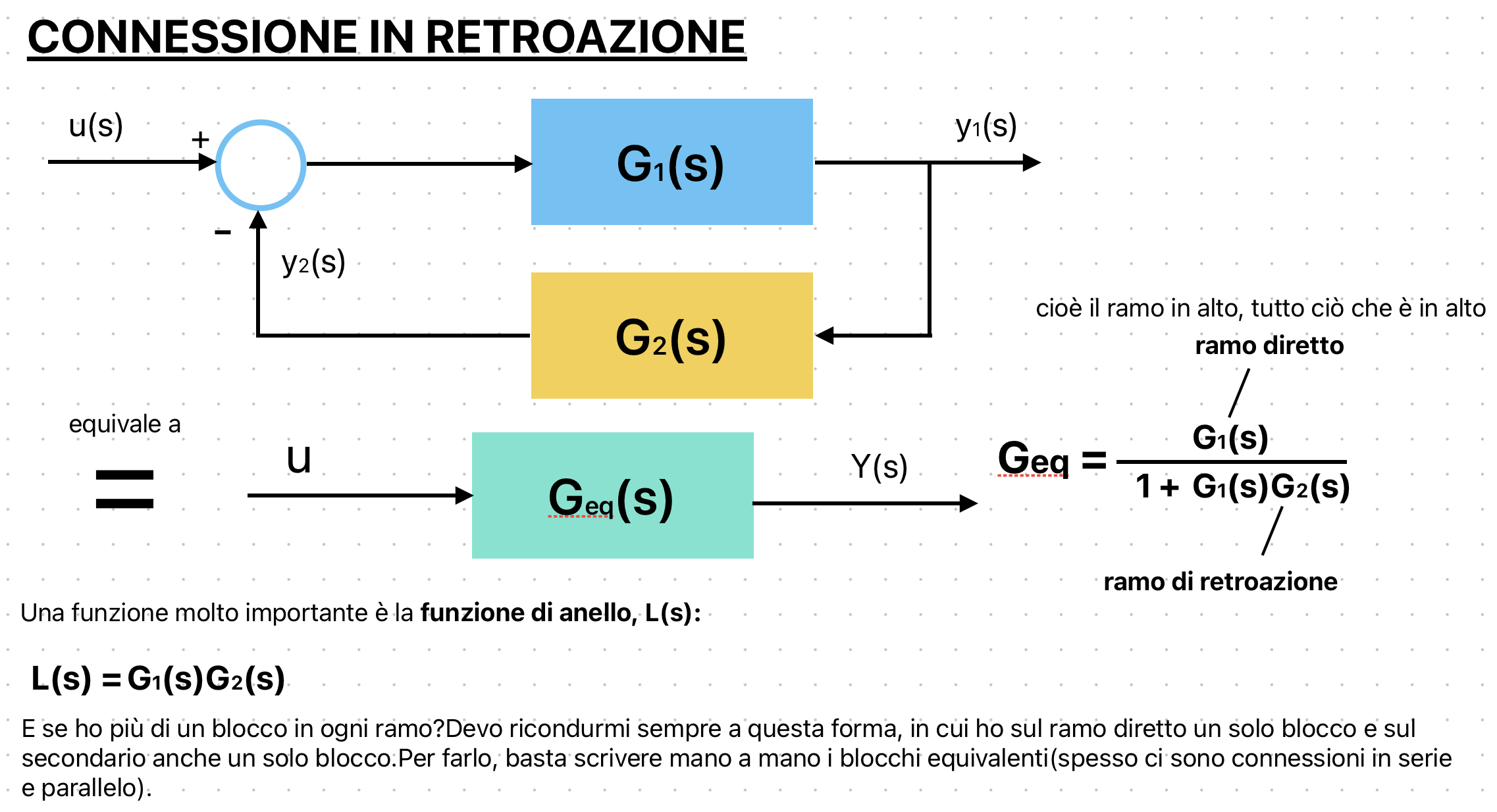
Quello riportato è uno schema di controllo in retroazione.Qui torna il discorso sul segnale di riferimento w(s), regolatore e andamento voluto. Come dicevamo, w(s) è l'andamento che desideriamo imporre al sistema controllato G(s) e vogliamo che l'errore di inseguimento,e(s) = w(s)-y(s) sia minimo.Graficamente, e(s) è quello che esce dal primo nodo sommatore sulla sinistra, dove entra w(s) positivo e y(s) invertito.

Ciò che impone a G(s) l'andamento è appunto R(s), cioè il regolatore.Come si può vedere ci sono anche i disturbi, n(s) che è l'errore di misura(nel cruise control errori nei sensori che riportano la velocità in retroazione per esempio), d(s) sono invece i disturbi dovuti all'ambiente esterno(nel cruise control potrebbe essere la pendenza della strada ad esempio).

Ora però dobbiamo capire come tutti gli ingressi(n(s),d(s),w(s)) influenzano il sistema in retroazione.Studiarli tutti insieme sarebbe molto complesso, per questo, useremo il Principio di Sovrapposizione Degli Effetti, che ci dice che possiamo studiare l'interazione del singolo ingresso nel sistema tenendo tutti gli altri spenti.Faremo questo con ogni ingresso e infine sommeremo tutti i contributi, di ogni ingresso e otterremo l'effetto complessivo. Questa è una proprietà dei sistemi lineari.

Definisco ramo diretto il prodotto R(s)G(s), cosi posso considerarlo come un blocco unico(infatti sarebbe la serie di due blocchi) e lo chiamo L(s).



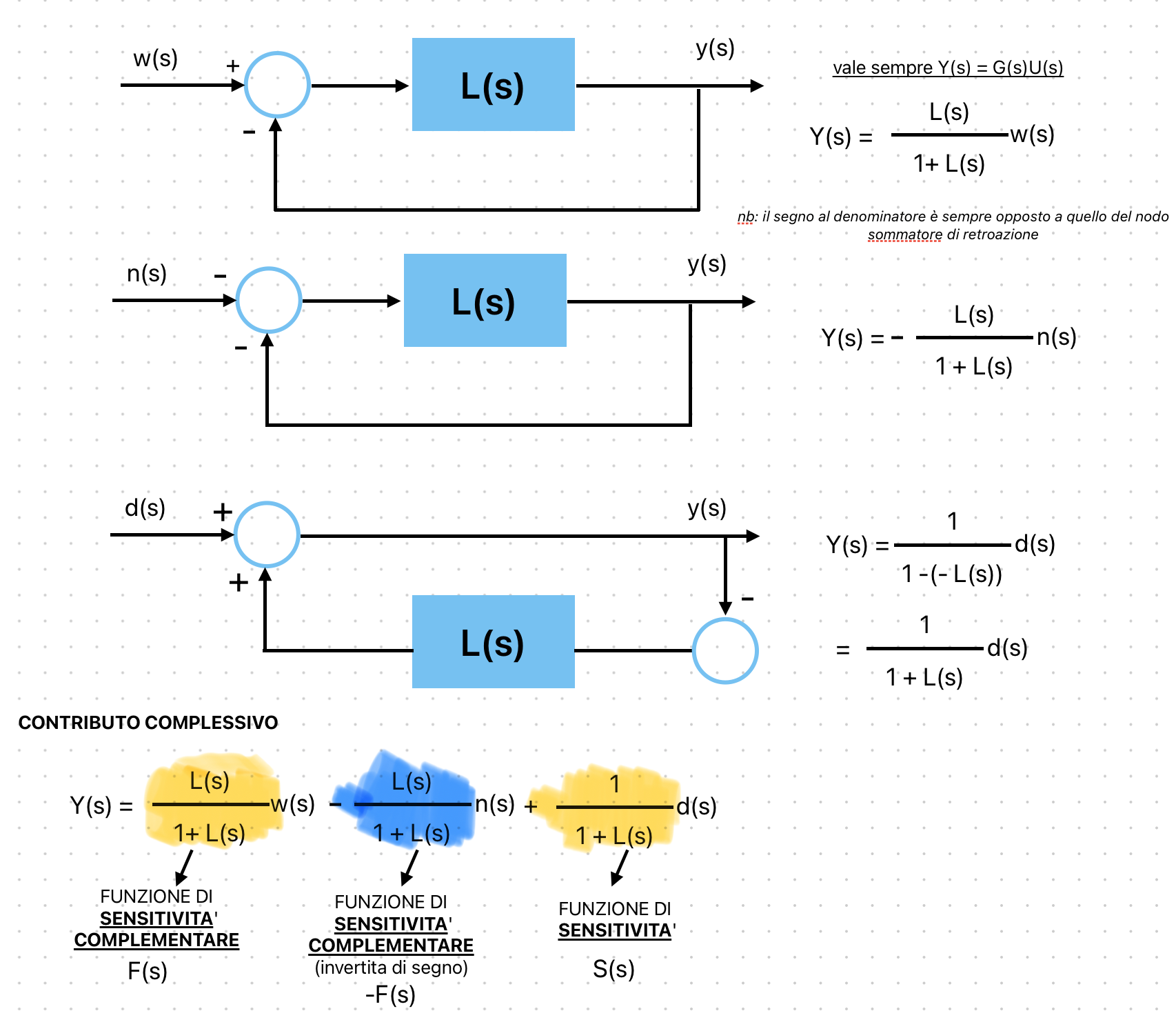
Si possono fare gli stessi calcoli con l'errore di inseguimento, e(s):



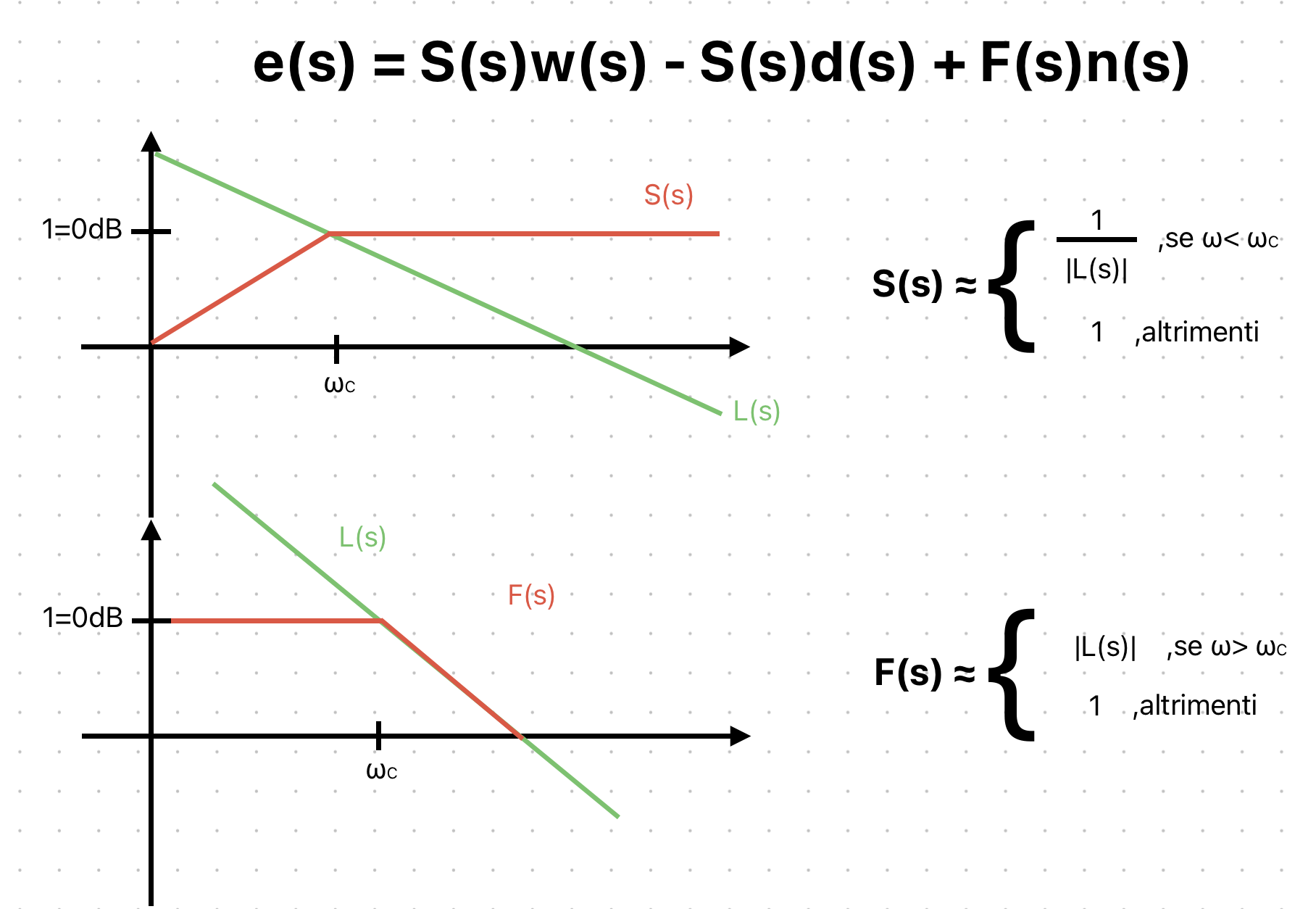
Questi concetti ci serviranno per il progetto, ma intanto facciamo alcune considerazioni su F(s) e su S(s). Nel progetto ci verrà richiesto di attenuare i disturbi, per farlo, useremo queste due funzioni. In particolare, questi disturbi sono segnali sinusoidali che entrano nel sistema, e ci viene chiesto di ridurre l'ampiezza delle oscillazioni. Questo può essere fatto tramite queste funzioni e usando l'approssimazione mostrata di F(s) e S(s).
Si noti come S(s) riduca le basse frequenze e F(s) quelle alte.

•Criterio di Nyquist: prendiamo il diagramma di Nyquist del sistema e individuiamo sull'asse reale il valore -1. Questo è detto punto critico, perchè annulla la funzione di anello a denominatore(1+L(s)).Chiamiamo P il numero di poli instabili. N è i il numero di giri che fa il diagramma attorno al punto critico(-1). Se P=N il sistema retroazionato sarà asintoticamente stabile.
•Critrerio di Bode: applicabile se P = 0, L(s) taglia l'asse in un solo punto(pulsazione critica unica), L(s) strettamente propria (grado denominatore > grado numeratore). Allora se ciò si verifica posso applicare il criterio(altrimenti devo provarne un'altro). Se posso applicarlo, dirò che il sistema retroazionato è as. stab se il guadagno statico è positivo e il margine di fase è maggiore(uguale) di zero.

Questi due criteri ci permettono di capire se il sistema retroazionato è stabile o meno, e il nostro obbiettivo è proprio avere un sistema asintoticamente stabile in retroazione.Spieghiamo ora cos'è il margine di fase.

Il margine di fase è una misura di quanto il sistema sia stabile:indica quanto il sistema è lontano dall'instabilità: un margine di fase più grande implica un sistema più stabile, mentre un margine piccolo (vicino a 0°) indica che il sistema è vicino all'instabilità.
E' ottenuto sottraendo a 180 il valore della fase alla pulsazione critica, cioè 180-arg(G(jω_c)).Approssimativamente si può stimare dai grafici, ma meglio prestare attenzione alle approssimazioni(ricordiamoci che il diagramma di Bode che disegnamo è già un andamento asintotico).
Quando il margine di fase è < 75°, ci sono delle oscillazioni.

Inoltre, spesso si può aggiungere un ritardo di tempo, che ritarda l'inizio dell'input, e quindi la risposta. Basta moltiplicare G(s) per e^(-sT) dove T è il valore del ritardo di tempo in secondi. Questo introduce ovviamente un cambiamento nel diagramma di fase, che viene tutto abbassato di un valore pari a (180/π) * ω_c * T.

Progettare un Regolatore

Ricapitolando, sono 3 le cose che guardiamo in un sistema retroazionato e quindi quando andiamo a progettare il regolatore R(s): asintotica stabilità(con i criteri visti), prestazioni statiche e prestazioni dinamiche.

Quando dobbiamo progettare un regolatore, ci vengono date delle specifiche, ossia delle caratteristiche che questo regolatore dovrà avere. In particolare, come strategia adotteremo quella di progettare la funzione di anello L'(s), partendo da quella del sistema già presente, L(s) e la modificheremo in modo da rispettare le specifiche.

Le prestazioni statiche riguardano l'errore di inseguimento e l'attenuazione dei disturbi di cui parlavamo prima, quando entrava un segnale sinusoidale.
Le prestazioni dinamiche riguardano invece lo smorzamento, il margine di fase, poli e zeri, sovraelongazione...

Prendiamo adesso un esercizio di progetto, che ci fornisce le seguenti specifiche:

•sistema da controllare: G(s) = -12 (s + 3)(s + 10)

•errore di inseguimento a tempo infinito e_∞(s) <= 0.1 a fronte di ingresso w(t) = 10sca(t)

•attenuazione disturbi n(s) = 1*sen(ωt) inferiore a 0.03 nella banda ω ϵ [60,∞)

•attenuazione disturbi d(s) = 1*sen(ωt) inferiore a 0.1 nella banda ω ϵ [0,1]

•banda passante superiore a 5

•margine di fase maggiore di 45 gradi

La prima cosa da fare è tradurre le specifiche, iniziando dall'errore di inseguimento. Ci viene chiesto di avere un errore di inseguimento a infinito(una volta esaurito il transitorio quindi) inferiore a 0.1.
Si può usare questa "formula" per calcolarlo:



Sappiamo che la trasformata di w(t)=10sca(t) è w(s) = 10/s, n è l'esponente che si trova sulla trasformata dell'ingresso(quindi è un valore noto), g è un valore incognito che dobbiamo ottenere e A è l'ampiezza dell'ingresso, in questo caso 10 perchè avevamo w(t) = 10sca(t).
Quindi da questo limite ricaviamo g che ci conviene imporre e soprattutto il guadagno statico μ, eguagliando il limite al valore di |e| richiesto. A primo impatto, potremmo pensare di scegliere una g molto alta, cosi da avere errore di inseguimento pari a 0.

Poi passiamo alle attenuazioni dei disturbi.Come già detto abbiamo un segnale sinusoidale in ingresso e dobbiamo fare in modo che il sistema non passi su questi disturbi.Per calcolare l'altezza alla quale L(s) che progettiamo dovrà passare usiamo le 2 funzioni di sensività e di sensività complementare:



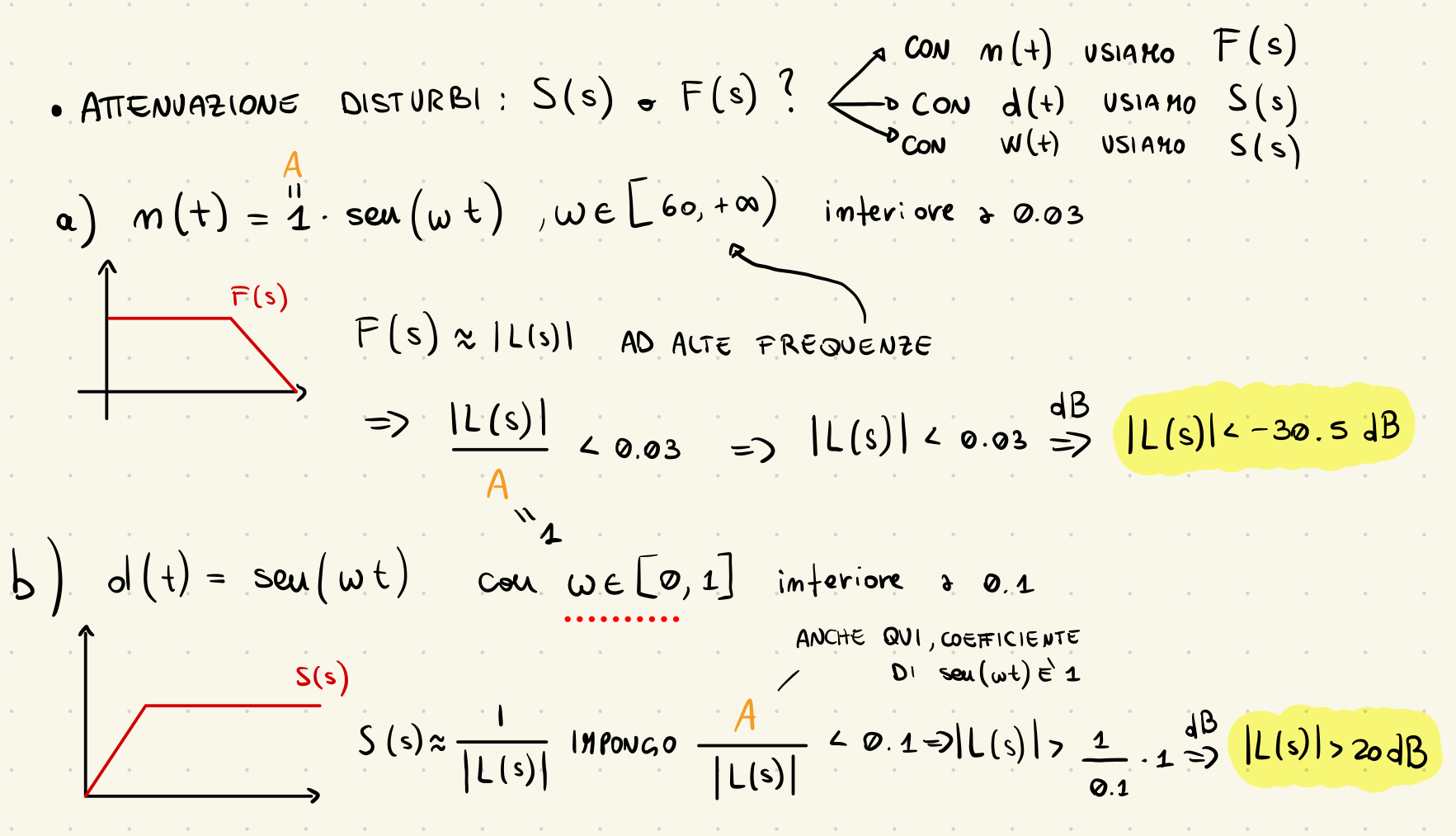
Come si vede la funzione di sensività complementare F(s) taglia i disturbi ad alte frequenze, mentre quella di sensitività S(s) taglia quelli a bassa frequenza.Tracciamo ora i vincoli sul Diagramma di Bode evidenziando le zone in cui non deve passare la nostra L(s):



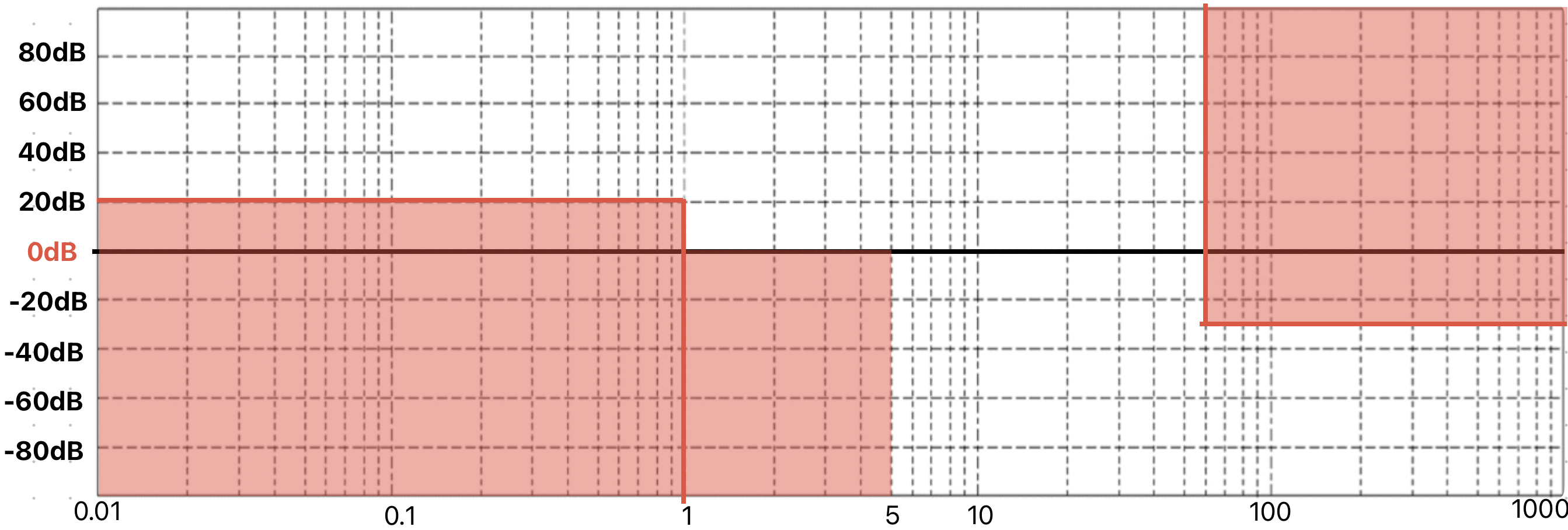
Quindi adesso ho calcolato tutto ciò che riguarda le prestazioni statiche: so già che devo partire con pendenza 0 e poi aggiungere poli e zeri quando andremo a vedere le prestazioni dinamiche. Per non passare sui disturbi, aggiungeremo poli e zeri.Le zone in rosso sono quelle su cui non devo passare. Tra 0 e 1 infatti devo rimanere sopra i 20dB, tra 1 e 5 sopra lo zero perchè la banda passante era superiore a 5 e tra 60 e infinito devo stare sotto i -30 dB come calcolato prima.

Poi devo assicurarmi sempre di avere un buon margine di fase, in questo caso ci viene proprio richiesto maggiore di 45. Per avere un margine di fase alto bisogna scegliere una pulsazione critica, o meglio, bisogna tagliare l'asse 0dB a pendenza -20dB/Dec. Andiamo prima a piazzare poli e zeri, poi vediamo come agire sul margine di fase.Ad ogni modo dovremmo già ottenere un buon margine di fase cosi.



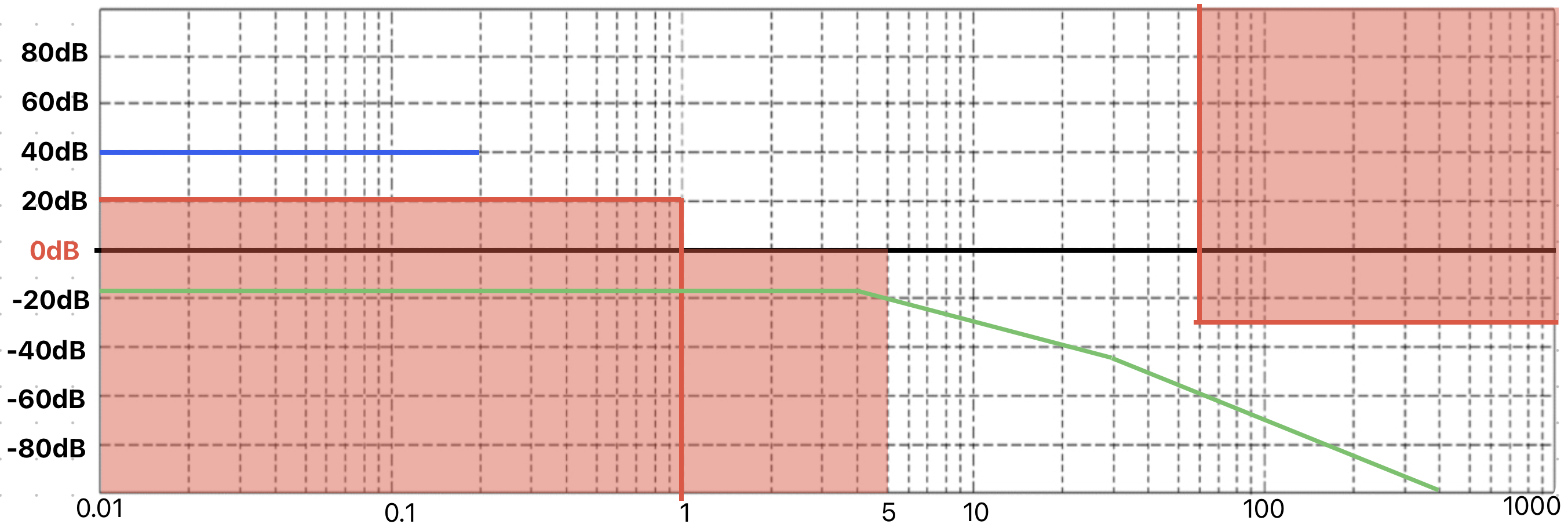
Sappiamo che dobbiamo iniziare con una pendenza 0. Quindi iniziamo a tracciare una retta orizzontale, in modo che su ω = 1 ci troviamo all'altezza del guadagno statico calcolato nell'errore di inseguimento.Anche se inserendo poli e zeri non passerà più per il guadagno statico, l'importante è che lo faccia senza. Poi aggiungiamo poli e zeri per evitare le zone dei disturbi, perchè sappiamo che i poli fanno scendere la pendenza e gli zeri la alzano:



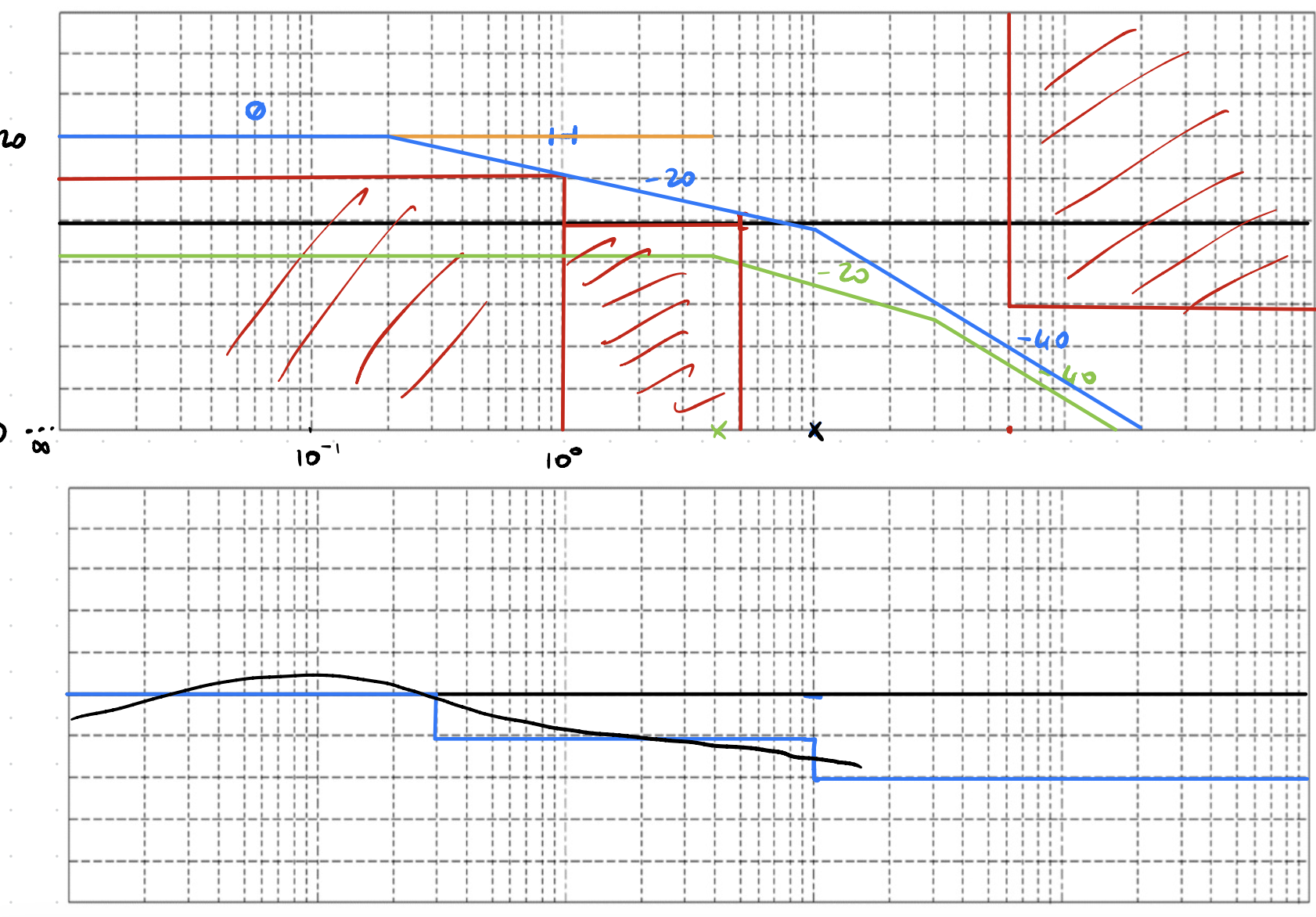
In verde troviamo disegnata la G(s).Da li infatti riusciamo a capire quali modifiche fare.Infatti l'abbiamo "alzata" e adesso abbiamo aggiunto poli e zeri che evitano il passaggio nelle "zone proibite". Adesso che ho disegnato la nuova L(s),quella blu, devo trovare l'espressione del regolatore R(S), ma prima devo ricalcolare il guadagno statico della funzione disegnata.Lo lascio incognito e impongo μ uguale al limite della nuova L(s) per s che tende a zero. Fatto questo, R(s) = L'(s)/G(s). Poi calcolo il margine di fase, come 180 meno valore assoluto dell'argomento di L'(jω_c) che sarà quindi un numero complesso, mi basta semplicemente calcolare l'argomento di questo numero. Se è superiore a 45°, ho posizionato correttamente poli e zeri e ho rispettato a questo punto tutte le specifiche richieste.Abbiamo tracciato inoltre il diagramma della fase.

Il margine di guadagno è un'altro parametro utile, mi dice di quanto il sistema può aumentare il proprio guadagno prima di diventare instabile, e si calcola come k𝑚 = 1 / |L(jω_π)| , cioè il reciproco del modulo di L(jω) quando ω = 180°=π.



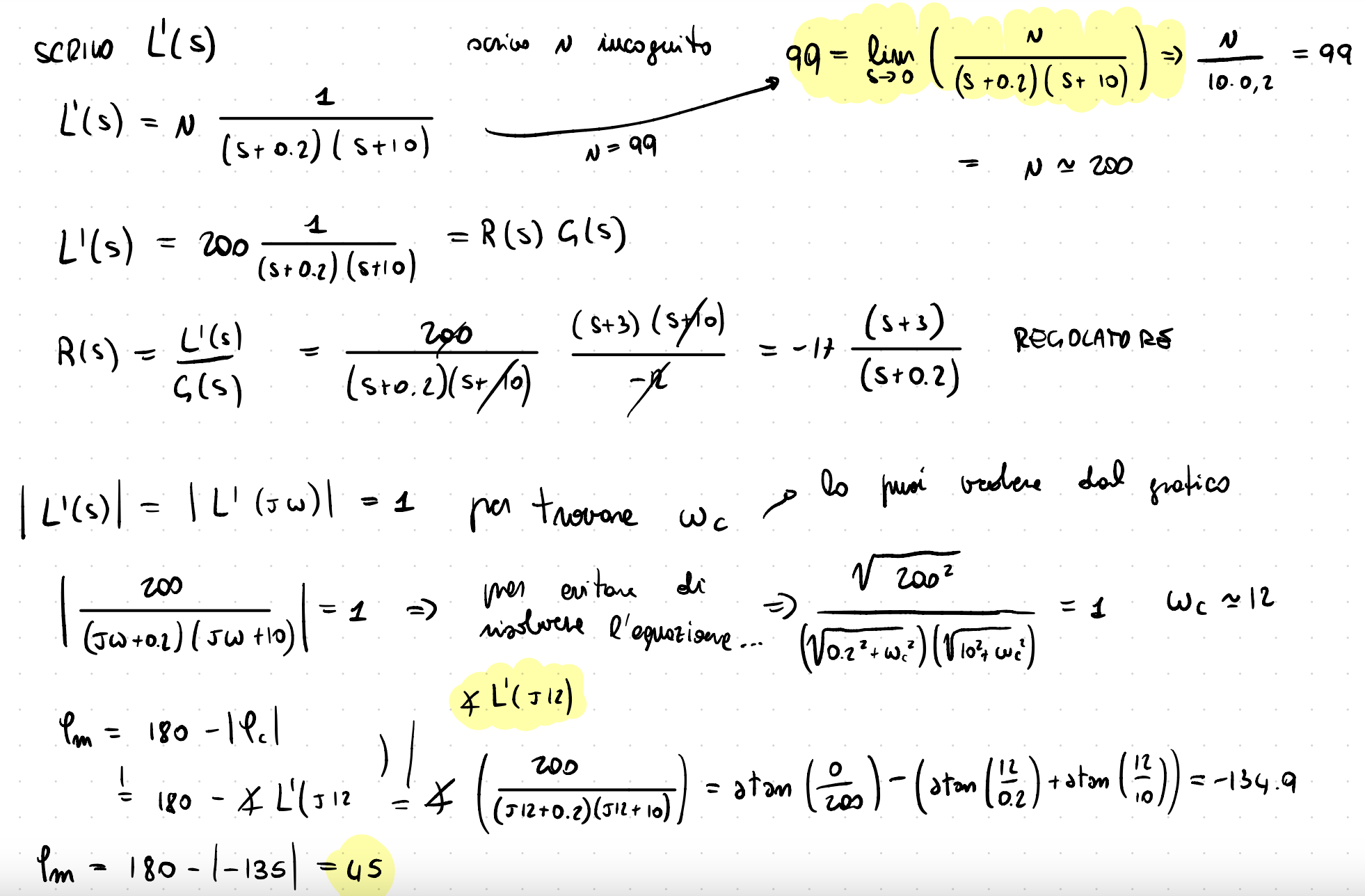
In generale, per un eventuale esame quello che conta è non passare sui disturbi, avere un buon margine di fase e rispettare l'errore di inseguimento.

Ecco uno schema riassuntivo:



Vediamo adesso alcuni esercizi che escono spesso durante gli esami:

1-Ci viene chiesto di dire un sistema che non è lineare è stabile. Quello che si fa allora è linearizzare l'equazione dello stato e valutare i coefficienti della matrice A con i criteri che abbiamo detto nella sezione dedicata alla stabilità.

2-Ci viene chiesta l'applicabilità secondo il criterio di Bode di un dato sistema inserito in retroazione in cui nel ramo diretto troviamo due blocchi in serie: uno che è semplicemente k e un'altro G(s), cioè il sistema dato, quindi l'uscita sarà kG(s), cioè k non fa altro che spostare il guadagno statico del sistema G(s). A questo punto possiamo vedere dai diagrammi di Bode quando spostando il guadagno si arriva ad avere che il criterio di Bode non è applicabile, ad esempio se abbassa tutto il grafico sotto gli 0dB vuol dire che non avrò più una pulsazione critica perchè è tutto sotto gli 0dB.A quel punto il criterio non sarà applicabile e ho trovato la risposta.

3-Nel progetto del regolatore fare attenzione nella L'(s) a non mettere zeri e poli vicino alla pulsazione critica, perchè abbassiamo di tanto il margine di fase, specialmente mettendo un polo dominante.Dovremmo inserirli ad almeno una decade.