AC circuits

Now we will see circuits whose voltage and current values depend on time and have a certain periodic behavior.AC is used for electricity distribution lines and in our homes for many reasons.

Knowledge required:

trygonometric basics

complex numbers

INTERESTING FACT:WHY AC IS USED FOR DISTRIBUTION LINES?

As you will see in next articles, in distribution lines is used an high voltage, in order to reduce losses of power due to Joule Effect:

P=R*I^2

losses due to Joule Effect.This is the power that a resistor or a cable(real cables has resistance) dissipate in the form of heat.

So, there are 2 ways to reduce losses:increase the thickness of cables(it has an high cost) so that resistance will decrease or raising voltage(keeping constant the power) so that current will drop and as a result, power losses due to joule effect will be reduced.

Remember that resistance depends on 3 factors: length of the cable, its thickness and its resistivity(that depends on the material).

So, since it is convenient raising the voltage, companies have to do it by using transformer, a device that works only with AC.In Italy for example high voltage lines reaches a maximum of 600 000V.

RESISTANCE(First Ohm Law):

This is the law that binds the 3 factors:

p is the resistivity, l is the length and S the section of the cable.

R=\rho \space \frac{l}{S}

Introduction to Alternate Current

AC is a current/voltage that constantly change, describing a sine wave called sinusoid.

this is what a sinusoid looks like: the current changes constantly reaching a peak each period.Every sinusoid has a period, like all trygonometric functions.

sinusoid:v(t)=V_msin(\omega t+\phi)

where t is the time, ϕ is the phase, ω is the angular frequency.

This sinusiod repeats each T seconds.That T is the period.The frequency is 1/T and it is the number of cicles done in a second.For example in Italy frequency(f) is 50Hz, so the sinusoid will repeat 50 times in a second.

If we take 2 sinusoids:

v_1=sin(\omega t)\space and \space v_2=sin(\omega t +\phi)\space with \space \phi \not=0

We will say that v2 is ahead of v1, they’re out of phase of ϕ.

How we can solve a circuit in AC? operating with sinusoid is too difficult, so we have to use phasor,you will see how to transform a sinusoid into phasor.

It is just the exponential form of complex numbers.The only information you loss when passing into phasor is the angular frequency.Phasor does not consider time, in fact it is said that when you pass from sinusoid to phasor, you pass from time domain to phasors domain.Example with voltage:

(time \space domain)\space v(t)=V_m sin(\omega t+\phi) =>V_m e^{j\phi} \space(phasor)

where j is the immaginary unit.Here you pass from Real numbers to Complex numbers.You can now represent a voltage or a current with a revolving vector(on Gauss Plane).Remember: Vm is the maximum voltage reached.

Derivative of a phasor:

\frac{dv}{dt}=>j\omega V

Phasors are written with capital letter.

Integral of a phasor:

\int vdt=>\frac{V}{j\omega}

IMPEDANCE AND ADMITTANCE

Impedance and admittance are two important concepts in AC circuits since they allow you to use Kirchhoff laws and Ohm Law also on AC circuits with also 2 new components: the capacitor and the inductor. Impedance is the measure of the total opposition to current flow in a circuit, while admittance is the measure of the total ability of a circuit to allow current flow.

Impedance is represented by the symbol Z,measured in ohms. It is a complex quantity that includes both resistance and reactance. Reactance is the opposition to current flow caused by the presence of capacitance or inductance in a circuit.

Admittance is represented by the symbol Y, measured in siemens (S). It is also a complex quantity that includes both conductance and susceptance. Conductance is the ability of a circuit to allow current flow, while susceptance is the ability of a circuit to store energy.

The relationship between impedance and admittance is given by the equation:

Y=\frac{1}{Z}

In AC circuits, impedance and admittance can be used to analyze the behavior of circuits with capacitors and inductors. This is important for understanding the behavior of electronic devices and power systems that rely on these components.

We introduce now 2 components: the capacitor and the inductor(remember that their behavior is not the same as in DC,in AC they not close or open circuit!).Consider them as a resistance for now, but consider the fact that their impedance and admittance are different:

COMPONENT	Impedance	Admittance
Resistor	Z=R	Y=1/R
Inductor	Z=jωL	Y=1/(jωL)
Capacitor	Z=1/(jωC)	Y=jωC

where C is the capacity and L is the inductance.

Imagine that Z and Y are like R and G!

Parallel and series are the same as the linear circuits: Z series are just the sum of each Z,Y parallel are the sum of Y…

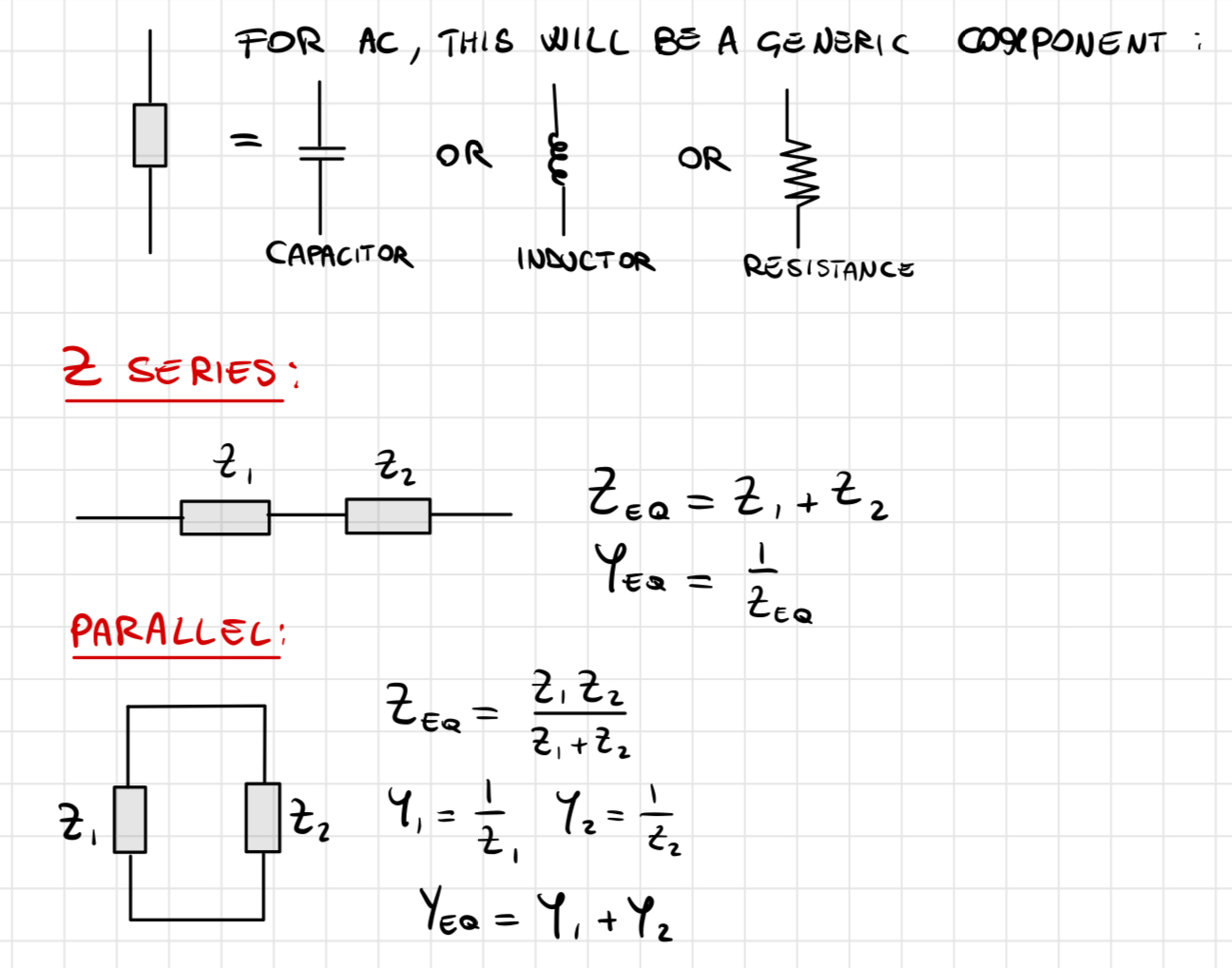
Since we can write Z as Z=R+jX where X is the immaginary part(due to the presence of capacitors or inductors),if X>0 your generic component would be equal to a inductor and if X<0, it would be equal to a capacitor.

Now, the good news is that you can use Kirchhoff laws,Norton and Thevenin like in the linear DC circuits.